Costruzione di mesh per il metodo dei volumi finiti. Metodo dei volumi finiti. Dividere il volume di un cubo in volumi finiti
Il vantaggio di questo metodo è che si basa su leggi di conservazione. Pertanto, a differenza del metodo delle differenze finite, il metodo del volume di controllo garantisce uno schema numerico conservativo, che consente di ottenere soluzioni accettabili in precisione anche su griglie relativamente grossolane.
L'idea principale del metodo è abbastanza semplice e facilmente suscettibile di interpretazione fisica. Quando si discretizzano le equazioni di Navier-Stokes mediate da Reynolds, il dominio computazionale è diviso in un gran numero di volumi elementari non sovrapposti, in modo che ciascun volume contenga solo un punto computazionale (nodale). L'insieme dei volumi elementari è chiamato mesh computazionale. Le celle della griglia possono avere forme diverse. I più comunemente usati sono gli esaedri (esaedri) e i tetraedri (tetraedri). Il metodo del controllo del volume consente l'utilizzo di celle con un numero arbitrario di facce (piramidi, prismi, poliedri complessi, ecc.).
La soluzione del sistema di equazioni (1)–(18) è rappresentata come un insieme di valori dei parametri desiderati ai centri di questi volumi. Ad esempio, se dividiamo il volume di una stanza in 1000 singoli volumi elementari (celle), allora come risultato della soluzione avremo 1000 valori di temperatura, velocità, pressione, ecc. In Fig. La Figura 2 mostra un frammento del dominio computazionale. Le celle sono numerate con indici io, j, k.
Riso. 2. Frammento del dominio computazionale
L'integrazione delle equazioni differenziali viene effettuata su ciascun volume elementare. Gli integrali vengono calcolati utilizzando formule di interpolazione, che vengono utilizzate per determinare i valori delle variabili desiderate tra i punti calcolati. Di conseguenza, si ottiene un analogo discreto delle equazioni originali nei punti nodali, che riflette la legge di conservazione delle variabili studiate in ciascun volume finito.
Va notato che nella maggior parte dei moderni pacchetti idrodinamici computazionali come “STAR-CD”, “FLUENT”, “CFX” e molti altri, il metodo del volume di controllo è implementato per discretizzare le equazioni del modello.
Griglie di calcolo
Il processo di costruzione di una mesh è uno dei momenti chiave nella conduzione di un esperimento numerico. Selezionare e costruire una griglia computazionale adeguata al problema in esame è una procedura piuttosto complessa e dispendiosa in termini di tempo. Una scelta razionale della mesh può semplificare notevolmente la soluzione numerica del problema.

Riso. 3. Configurazioni delle celle della griglia
Le celle della griglia possono avere forme diverse (Fig. 3) e dimensioni che si adattano meglio alla risoluzione di un problema specifico. Il tipo più semplice di griglia è quando le celle sono identiche e hanno una forma cubica.
Di norma, in prossimità di superfici solide la maglia diventa più densa, cioè le celle hanno una dimensione normale alla superficie più piccola. Questo viene fatto per migliorare la precisione dei calcoli in quelle aree dove i gradienti di flusso dei parametri studiati cambiano più rapidamente, ad esempio nello strato limite.
Puoi aumentare la precisione dei calcoli e ridurre l'errore di approssimazione in 2 modi:
· aumentare l'ordine di accuratezza del campionamento;
· diminuendo il passo della griglia.
Quando si risolvono problemi non stazionari, le dimensioni delle celle Δx e il passo di integrazione temporale Δt sono correlati alla condizione CFL (Courant-Friedrichs-Levy):  , tu- velocità.
, tu- velocità.
I programmi informatici universali attualmente utilizzati nella pratica ingegneristica consentono di lavorare su mesh arbitrarie non strutturate utilizzando elementi altamente distorti. In questo caso, l'ordine di precisione della discretizzazione, di regola, non supera il secondo. Per ottenere una soluzione di alta qualità è necessario costruire griglie computazionali con piccoli passaggi.
Il pacchetto STAR-CCM è passato all'uso di celle poliedriche (simili a un pallone da calcio) che, combinando le celle, eliminano l'aspetto di celle altamente distorte.
Il vantaggio principale delle mesh non strutturate rispetto a quelle regolari è una maggiore flessibilità nel discretizzare una regione fisica di forma complessa. In questo caso le celle della griglia devono avere volumi o aree comparabili e non devono intersecarsi. Tuttavia, gli svantaggi di questo tipo di rete includono un aumento della dimensione della rete. Come dimostra la pratica, per lo stesso oggetto, una mesh non strutturata, se costruita correttamente, ha circa il doppio delle celle di una strutturata, il che porta naturalmente ad un aumento del tempo di calcolo rispetto alle mesh regolari. Tuttavia, in molti casi, le mesh non strutturate rappresentano l’unica opzione di costruzione possibile a causa della complessità della geometria dell’oggetto. Inoltre, con una scelta razionale dell'algoritmo di meshing, il tempo impiegato per costruire una mesh non strutturata risulta essere significativamente inferiore al tempo richiesto per costruire una mesh strutturata (strutturata a blocchi). Di conseguenza, il tempo totale impiegato per risolvere il problema (incluso il tempo di creazione della mesh e quello di calcolo) può essere molto inferiore quando si utilizzano mesh non strutturate rispetto a quelle strutturate.
Determinare la dimensione della maglia richiesta è, di per sé, un compito molto difficile. Il metodo universale da seguire nella scelta della dimensione della griglia si basa sul fatto che la soluzione risultante non deve cambiare all'aumentare del numero di celle (convergenza della griglia).
Per i problemi tipici, non è necessario condurre uno studio sulla convergenza della griglia, poiché è possibile fare affidamento sui risultati ottenuti in precedenza. Quando si passa allo studio di un nuovo tipo di problema, è imperativo effettuare uno studio sulla convergenza della griglia e determinare i requisiti per la griglia computazionale.
Si noti che quando si risolvono problemi reali di ventilazione e condizionamento dell'aria, il numero caratteristico di celle va, di regola, da 500mila a 3-4 milioni, a seconda della complessità geometrica dell'oggetto, dell'insieme dei parametri richiesti e delle specificità di il problema. In questo caso, il tempo di calcolo su un cluster composto, ad esempio, da 24 core può arrivare fino a una settimana e, quando si risolvono problemi non stazionari, fino a diverse settimane.
Il pacchetto STAR-CCM+ include un modulo per la creazione di mesh computazionali. Esistono anche pacchetti separati per la generazione di mesh, ad esempio quello ampiamente utilizzato è ANSYS, ICEM CFD (ICEM). Le mesh costruite nei pacchetti esterni possono essere importate nel pacchetto STAR-CCM+.
Capitolo 1. Metodi per discretizzare i sistemi di leggi di conservazione.
1.1. Principi tecnologici dei metodi di discretizzazione per problemi ai valori al contorno iniziale utilizzando spazi agli elementi finiti.
1.1.1. Metodi degli elementi finiti.
1.1.2. Metodi ai volumi finiti.
1.2. Schemi controvento su griglie semplici.
1.3. Metodi per risolvere il sistema stazionario delle equazioni di Navier-Stokes.
Capitolo 2. Costruzione di analoghi discreti delle equazioni di reazione-diffusione convettiva utilizzando il metodo dei volumi finiti
2.1. Discretizzazione MKO/FE di problemi di tipo convettivo-diffusionale.
2.1.1. Triangolazione e metodo per costruire una doppia mesh.
2.1.2. Forma integrale delle leggi di conservazione.
2.1.3. Approssimazione dei flussi di diffusione e calcolo della matrice di rigidezza MKO/FE.
2.1.4. Approssimazione dei termini di origine.
2.1.5. Calcolo della matrice di massa MCO/FE.
2.1.6. Contabilità delle condizioni al contorno.
2.2. Costruzione di schemi controvento multidimensionali su griglie simpliciali.
2.2.1. Calcolo delle matrici convettive locali.
2.2.2. Schemi con pesatura di flussi di massa.
2.2.3. Modifica di schemi esponenziali.
2.2.4. Alcune proprietà degli schemi di controflusso e principi della loro costruzione.
2.2.5. Un analogo dello schema esponenziale per schemi con il calcolo delle incognite al centro delle celle.
2.3. Nuove classi di formule integrali MKO.
2.3.1. Integrazione di monomi di coordinate baricentriche.
2.3.2. Sulle possibili combinazioni di rappresentazioni polinomiali.
2.3.3. Sull'ordine crescente dei polinomi di interpolazione della rappresentazione della soluzione locale.
2.4.4. Utilizzo di elementi finiti incoerenti.
2.4. Assemblaggio per elementi di matrici globali
Capitolo 3. Modellazione del campo di moto di mezzi viscosi incomprimibili.
3.1. Modello matematico.
3.2. Forma integrale delle leggi di conservazione.
3.3. Tenendo conto della relazione tra velocità e campi di pressione.
3.3.1. Interpolazione di Ry-Chow per il calcolo dei flussi di massa.
3.3.2. Discretizzazione dell'equazione di continuità.
3.3.3. Contabilità dei confini con flusso di massa diverso da zero.
3.3.4. Schema generale di iterazione 1.
3.4. Accelerare la convergenza degli schemi iterativi.
3.4.1. Correzione dei campi di pressione e velocità
3.4.2. Schema generale di iterazione II.
3.5. Risoluzione di sistemi di equazioni algebriche lineari.
Capitolo 4. Esperimenti numerici.
4.1. Analisi di stabilità per soluzioni di tipo strato limite.
4.2. Flusso accelerato in un tubo tondo.
4.3. Flusso nel tratto iniziale di un canale liscio.
4.4. Flusso laminare di un getto da un ugello puntiforme (getto sorgente)
4.5. Flusso laminare dietro un gradino piatto asimmetrico
4.5.1. Calcolo utilizzando vari schemi a monte
4.5.2. Effetto di input quando si calcolano i flussi dietro un passo indietro utilizzando MKO/FE su griglie simpliciali.
4.5.3. Confronto tra diversi metodi per la risoluzione di sistemi di equazioni algebriche lineari.
Elenco consigliato delle tesi
Modellazione dei flussi interni di un fluido viscoso incomprimibile mediante il metodo degli elementi finiti utilizzando schemi di controflusso 2007, Candidata di scienze fisiche e matematiche Gobysh, Albina Vladimirovna
Schemi numerici basati su approssimazioni a volumi finiti/elementi finiti per la risoluzione di problemi di idrodinamica a onde lunghe 2004, candidato di scienze fisiche e matematiche Styvrin, Andrey Vadimovich
Tecnologie parallele per la risoluzione di problemi ai limiti 2005, Dottore in scienze fisiche e matematiche Vasilevsky, Yuri Viktorovich
Metodo dei volumi finiti per problemi di convezione-diffusione e modelli di flusso bifase 2010, Candidato di scienze fisiche e matematiche Nikitin, Kirill Dmitrievich
Modellazione tridimensionale dei processi di trasferimento delle impurità in mezzi porosi di struttura complessa 2007, Candidato di scienze fisiche e matematiche Kapyrin, Ivan Viktorovich
Introduzione della tesi (parte dell'abstract) sul tema “Tecnologie del metodo dei volumi finiti/elementi finiti su griglie simpliciali per problemi di tipo convettivo-diffusorio”
La soluzione numerica di problemi di fisica matematica è uno dei principali metodi per studiare i fenomeni reali. L'uso combinato di esperimenti computazionali e fisici nell'analisi di qualsiasi fenomeno consente, da un lato, di ridurre il numero di costose misurazioni sperimentali e, dall'altro, di verificare e migliorare i modelli matematici.
Con l'aumento della velocità dei sistemi informatici, vengono poste nuove esigenze sui metodi numerici per risolvere problemi di fisica matematica. Lo sviluppo e il miglioramento di metodi moderni per la discretizzazione delle leggi di conservazione, che offrono la possibilità di simulare classi di problemi sempre nuove e ottenere risultati significativamente migliori nella risoluzione di quelli noti, è un'importante area di ricerca.
I moderni algoritmi computazionali dovrebbero fornire la descrizione più accurata delle aree con geometria complessa. Ciò è possibile utilizzando mesh non ortogonali e non strutturate. Rispetto alle mesh arbitrarie non ortogonali, per le mesh simpliciali non strutturate (triangolazione nel caso bidimensionale e partizione in tetraedri nel caso tridimensionale), le condensazioni locali sono più facili da implementare (ad esempio, dietro un gradino, in una zona di restringimento improvviso, in prossimità del punto di attacco), ed anche, se necessario, adattamento della griglia di calcolo in funzione del comportamento della soluzione. Pertanto, anche quando si discretizzano le leggi di conservazione in domini geometricamente semplici che possono essere rappresentati accuratamente da una raccolta di elementi rettangolari, le mesh semplici non strutturate presentano una serie di vantaggi. Nonostante gli evidenti vantaggi delle griglie non strutturate per l’approssimazione di regioni arbitrarie e la possibilità di costruire automaticamente partizioni semplici, esse non sono state praticamente utilizzate nella fluidodinamica computazionale e solo negli ultimi 15 anni sono diventate sempre più popolari. Secondo la testimonianza di B. Stoufflett et al., la ragione di ciò è il forte aumento dei tempi di calcolo quando si passa ad approcci non strutturati. Il fatto è che la posizione degli elementi diversi da zero nelle matrici degli analoghi discreti dipende dalla contiguità dei nodi della griglia e, arbitrariamente, le matrici vengono memorizzate utilizzando formati e strutture dati universali. Le operazioni di moltiplicazione di una matrice sparsa per un vettore e di fattorizzazione incompleta diventano molto più “costose”. Allo stesso tempo, i sistemi di equazioni della fluidodinamica computazionale sono sistemi di equazioni non lineari interconnessi, i cui schemi di soluzione implicita hanno una natura iterativa multilivello, per cui ad ciascuna delle iterazioni “globali” è necessario risolvere diversi sistemi di equazioni algebriche lineari. È stato con l'avvento di potenti sistemi di calcolo, nonché grazie allo sviluppo di metodi adattivi e multigrid, che è diventato possibile utilizzare griglie non strutturate e corrispondenti schemi di discretizzazione spaziale per modellare i processi idrogasdinamici.
Il metodo di discretizzazione più comune nel caso non strutturato è il metodo degli elementi finiti (FEM). Notiamo vantaggi del metodo come la conservazione della natura simmetrica della parte autoaggiunta degli operatori differenziali nei loro analoghi discreti (questo si ottiene mediante una scelta speciale dello spazio delle funzioni di test che coincide con lo spazio delle funzioni di prova) , la possibilità di aumentare la precisione dell'approssimazione aumentando il grado di interpolazione dei polinomi della rappresentazione della soluzione locale (le cosiddette versioni p e h-p di FEM, ), naturale considerazione delle condizioni al contorno del secondo e terzo tipo. In particolare il metodo degli elementi finiti ha una base tecnologica consolidata
Metodi per approssimare i prodotti interni presupponendo una rappresentazione polinomiale a tratti della soluzione e dei parametri di un problema ai limiti, vale a dire: l'uso della decomposizione in base dello spazio degli elementi finiti corrispondente, classi di formule integrali che consentono di integrare accuratamente arbitrari prodotti di funzioni di base su elementi di partizione e bordi (facce) di elementi,
Apparato di interpolazione standard.
Le tecnologie del metodo consentono di costruire in modo semplice e uniforme analoghi discreti di problemi ai valori al contorno iniziali, con vari tipi di condizioni al contorno presupponendo un certo grado di levigatezza della soluzione e comportamento polinomiale a tratti dei coefficienti delle equazioni e condizioni al contorno , .
In una serie di applicazioni, come la modellazione di flussi di gas supersonici e transonici e i calcoli utilizzando modelli di acque poco profonde, il conservatorismo locale degli schemi utilizzati per discretizzare le leggi di conservazione è molto importante. Il metodo degli elementi finiti non consente di tracciare con soddisfacente accuratezza le caratteristiche delle soluzioni discontinue emergenti, e l'approccio tradizionale alla risoluzione di tali problemi è il metodo dei volumi finiti. Quando si discretizza un sistema di leggi di conservazione con il metodo dei volumi finiti, il dominio computazionale viene approssimato da un insieme di volumi finiti aperti, quindi il ricercatore fa un “passo indietro”, passando alla forma integrale del sistema di equazioni originale; Utilizzando la formula di Ostrogradsky-Gauss, passiamo dall'integrazione del volume all'integrale al contorno, in modo che il metodo di approssimazione dei flussi attraverso le facce dei volumi finiti determini completamente lo schema computazionale. Secondo la monografia di S. Patankar, "per la maggior parte dei ricercatori che lavorano nel campo dell'idrodinamica e del trasferimento di calore, il metodo degli elementi finiti sembra ancora avvolto nel mistero. La formulazione variazionale e persino il metodo Galerkin non si prestano a una semplice interpretazione fisica". Allo stesso tempo, gli schemi a volumi finiti hanno un certo significato fisico dell’equilibrio dei flussi e dei termini di sorgente in ciascuno dei volumi finiti che si avvicinano al dominio computazionale, il che rende il metodo dei volumi finiti più attraente. La “semplicità” di MKO è una delle ragioni della mancanza di una base tecnologica generale per il metodo.
Quindi, i vantaggi della versione classica del MKO (metodo dei volumi finiti/differenze finite, FVDM) includono il conservatorismo locale degli schemi discreti, una maggiore semplicità e chiarezza e la possibilità di tenere naturalmente conto delle condizioni al contorno del secondo tipo. Inoltre, nel caso di risoluzione di problemi con predominanza della convezione, l'implementazione di schemi di controflusso è semplificata, poiché i flussi attraverso le facce di volumi finiti sono sia quantità analizzate che approssimate.
I tentativi di sistematizzare le approssimazioni dei volumi finiti hanno portato a una parziale combinazione di tecnologie FEM e principio di integrazione su volumi finiti; i primi risalgono al lavoro di B. R. Baliga, K. Prakash e S. Patankar e sono conosciuti come metodi CVFEM (metodi agli elementi finiti basati sul volume di controllo), di seguito denominati metodi volume finito/elementi finiti (FVM/ FE). Gli autori del metodo hanno perseguito l'obiettivo di costruire schemi conservativi del metodo dei volumi finiti, utilizzando uno dei principali vantaggi del FEM: la capacità di approssimare geometrie complesse utilizzando mesh non strutturate. Le funzioni di profilo in questa classe di metodi sono “di natura ausiliaria”; non viene sottolineata l'appartenenza della soluzione a spazi ad elementi finiti. Gli insiemi baricentrici vengono utilizzati come doppia partizione.
Per la prima volta, il problema della mancanza di principi tecnologici universali del metodo dei volumi finiti/differenze finite (MKO/KR, FVDM) viene discusso nel lavoro di Z. Kaya “Sul metodo dei volumi finiti/elementi”. L'autore attira l'attenzione del lettore sulla "natura non sistematica del metodo dei volumi finiti/delle differenze finite"; Quando si approssimano sistemi di leggi di conservazione con il metodo dei volumi finiti/differenze finite, è possibile utilizzare approssimazioni di classi diverse all'interno dello stesso lavoro, il che complica notevolmente l'analisi della convergenza di tali schemi. Viene proposta una soluzione a questo problema: l'uso congiunto delle idee del metodo degli elementi finiti (ricerca di una soluzione in uno spazio di elementi finiti e utilizzo del comportamento polinomiale a tratti della soluzione per calcolare i flussi) e della forma integrale delle leggi di conservazione. Pertanto, i metodi volume finito/elemento (FME/E, “metodi box”, FVE) sono nati nel tentativo di creare “tecnologie a volume finito più sistematiche”. L'assenza di principi tecnologici generali dei metodi dei volumi finiti/delle differenze finite è notata anche nei lavori di Ya.JI. Guryeva e V.P. Ilyin.
I metodi volume finito/elementi finiti (FVE) e metodi volume finito/elementi finiti (CVFEM) utilizzano spazi di elementi finiti coerenti di funzioni lineari su simplessi e appartengono alla classe degli schemi di volume finito cella-vertice, Fig. 1, a.
Un certo numero di schemi di fluidodinamica computazionale (modellazione di flussi viscosi incomprimibili) utilizzano spazi di elementi finiti incoerenti, in particolare, lo spazio lineare di Crousey-Raviard su elementi continui ai centri dei bordi delle funzioni di test. I metodi ai volumi finiti che utilizzano spazi di elementi finiti incoerenti sono stati proposti da S. Choi e D. Kwak, studiati in numerosi lavori di altri autori (i cosiddetti metodi dei sottovolumi, metodo del covolume) e sono schemi con il calcolo delle incognite ai centri dei bordi ( Gli schemi più comuni per risolvere problemi di dinamica dei gas e modellare i disastri di origine antropica utilizzando equazioni di acque poco profonde sono schemi a volumi finiti centrati sulla cella, Fig. 1, f. La loro popolarità è dovuta al fatto che nel caso del calcolo delle incognite nei centroidi, la maggior parte degli schemi di dinamica dei gas (schemi S.K. Godunov, schemi TVD) possono essere trasferiti a reti non strutturate senza cambiamenti tecnologici fondamentali. o un dentro Fig. 1. Posizione dei punti di calcolo rispetto ai nodi della griglia FE. In questo lavoro si considerano principalmente classi di metodi ai volumi finiti con calcolo delle incognite ai nodi di triangolazione (MKO/E, MKO/FE) e ai centri di bordo (metodi ai sottovolumi); in futuro diremo anche “metodi ai volumi finiti che utilizzano spazi di elementi finiti”. " Queste classi di metodi, secondo numerosi studi (, ), per problemi di convezione-diffusione forniscono migliori approssimazioni alla soluzione rispetto ai metodi con il calcolo delle incognite al centro delle cellule. Uno dei motivi principali è che per i metodi sopra elencati viene preservata la continuità delle derivate prime delle funzioni di test sugli elementi della doppia mesh. Un approccio efficace alla risoluzione dei problemi con predominanza della convezione è l'uso del metodo Galerkin con funzioni di test simmetriche per la parte autoaggiunta degli operatori differenziali e schemi MCO a monte per la loro parte asimmetrica, la cosiddetta. metodi misti elementi finiti/volume (FEM/O, MEV, metodo misto elementi/volume). Il lavoro di tesi è dedicato, in particolare, al miglioramento delle tecnologie del metodo dei volumi finiti per le classi di metodi indicate (metodi MKO/E, MKO/CE, FEM/O, metodi a sottovolumi). Al momento, questi metodi non dispongono di tecnologie consolidate per tenere conto del comportamento polinomiale a tratti della soluzione, dei termini sorgente e dei coefficienti di trasferimento. Possiamo elencare le seguenti ragioni per l'imperfezione dell'apparato per l'esatta integrazione dei polinomi nei metodi ai volumi finiti che utilizzano spazi degli elementi finiti: 1. A differenza del metodo degli elementi finiti, il metodo dei volumi finiti non ha una versione p, poiché con l'introduzione di nodi aggiuntivi e diversi tipi di maglie doppie, il conservatorismo locale di un numero di variabili del sistema di leggi di conservazione in relazione a volumi finiti “alieni” viene violata. Pertanto, le approssimazioni sono limitate agli spazi degli elementi finiti di ordine inferiore. 2. Rispetto al metodo degli elementi finiti, i metodi ai volumi finiti sono caratterizzati da una maggiore libertà nella scelta degli spazi delle funzioni test, che in questo caso risultano essere legate alla localizzazione dei punti di calcolo delle incognite rispetto alla discretizzazione nodi (schemi con la posizione delle incognite nei nodi, punti medi dei bordi, centroidi simplex) e il metodo di costruzione di una doppia griglia (utilizzando insiemi baricentrici, ortocentrici e circocentrici). Combinato con la possibilità di utilizzare griglie collocate o sfalsate, ciò offre l'intera varietà di schemi MCM esistenti in ciascuna applicazione. Per i metodi MCM per discretizzare le leggi di conservazione che utilizzano spazi di elementi finiti, un'attenta selezione di questi spazi per soluzioni, coefficienti di equazioni e termini sorgente perde in parte il suo significato se il metodo non ha sviluppato mezzi per tenere conto delle rappresentazioni polinomiali a tratti, in particolare , l'apparato per l'integrazione esatta di polinomi su elementi della doppia mesh, sottodomini di elementi e segmenti di bordi di confine. Di conseguenza, i risultati dei calcoli utilizzando gli schemi costruiti dovrebbero essere considerati dal punto di vista degli effetti dell'integrazione numerica, tenendo conto dei vari metodi della loro implementazione; diventa significativamente più difficile confrontare i risultati della ricerca con i lavori di altri autori, ecc. Pertanto, questo lavoro è dedicato alla revisione delle tecnologie MCM/FEM esistenti per la costruzione di analoghi discreti di problemi di tipo convezione-diffusione. La tecnologia per tenere conto della rappresentazione polinomiale a tratti della soluzione, dei coefficienti dell'equazione e di quelli inclusi nelle condizioni al contorno, nonché dei termini di origine nei metodi ai volumi finiti che utilizzano spazi di elementi finiti deve soddisfare i seguenti requisiti: 1) consentire combinazioni arbitrarie di rappresentazioni polinomiali di coefficienti e soluzioni su elementi di partizione, nonché aumentare il grado di interpolazione dei polinomi della rappresentazione della soluzione locale; 2) utilizzare principi unificati di approssimazione nel calcolo dei contributi degli elementi corrispondenti a vari termini dell'equazione (diffusione, convezione, termini di reazione, termini di sorgente), nonché contributi da bordi che approssimano parti di confini con diversi tipi di condizioni al contorno specificate su di essi; 3) consentire una generalizzazione omogenea al caso tridimensionale; 4) tenere conto dell'esperienza di tecnologie degli elementi finiti ben sviluppate, in particolare, dell'uso dell'espansione di base degli spazi degli elementi finiti e dei vantaggi dell'integrazione accurata delle rappresentazioni polinomiali a tratti della soluzione e dei coefficienti di trasferimento; 5) fornire una base tecnologica unificata per approssimazioni miste FEM/O che utilizzano due insiemi di funzioni di test - volume finito ed elemento finito - per approssimare un'equazione; 6) i principi della tecnologia dovrebbero rimanere invariati durante la transizione dall'uso di spazi coerenti agli elementi finiti (metodi a volumi finiti/elementi finiti con calcolo delle incognite ai nodi) all'uso di elementi finiti inconsistenti (metodi con calcolo delle incognite ai centri dei bordi di triangolazione); 7) la tecnologia può essere utilizzata per approssimare varie classi di problemi fisici. Delle tecnologie esistenti dei metodi dei volumi finiti che utilizzano spazi degli elementi finiti (metodi volume finito/elemento finito (FVE), metodi volume finito/elemento finito (CVFEM), metodi sottovolume, metodi volume/elemento misto (MEV)), nessuna non soddisfa i requisiti di cui sopra. Pertanto, la creazione di nuove tecnologie per queste classi di metodi che utilizzano partizioni simpliciali e insiemi baricentrici come duali sembra essere un argomento di ricerca rilevante. Nel caso di una predominanza significativa della convezione, il confronto tra vari schemi di discretizzazione MCO, nonché il confronto dei calcoli utilizzando il metodo degli elementi finiti e il metodo dei volumi finiti, si riduce in realtà al confronto dei corrispondenti schemi controvento. I più studiati e spesso utilizzati nel caso non strutturato sono gli schemi controvento della classe dei metodi a volumi finiti con il calcolo delle variabili al centro delle celle. Nonostante i bordi degli elementi di partizione non siano paralleli agli assi coordinati, questi schemi nella maggior parte dei casi sono di natura unidimensionale, poiché si riducono a risolvere il problema del decadimento di una discontinuità sulle linee che collegano gli elementi centroidi dei simplessi. I calcoli che utilizzano tali schemi non riproducono la struttura multidimensionale del flusso e hanno una diffusione numerica eccessiva. Per costruire a monte schemi di approssimazione del secondo ordine è necessaria una significativa espansione del modello, che nel caso non strutturato porta ad una significativa complicazione delle corrispondenti strutture dati. Gli schemi a monte per gli schemi con il calcolo delle incognite nei nodi di triangolazione e nei punti medi dei suoi bordi sono attualmente pochi (vedi). In alcuni casi, il principio di approssimazione a monte si riduce all'utilizzo di un valore di una sostanza scalare - in un nodo simplex che si trova a monte, o di due valori ponderati - alle estremità di un bordo simplex che si trova a monte. Solo uno degli schemi conosciuti, il FLO (Flow Oriented Upwind Scheme), sviluppato da K. Prakash e S. Patankar, sfrutta il calcolo delle incognite ai nodi - la capacità di costruire funzioni di profilo asimmetriche. Ma i calcoli che utilizzano questo schema sono considerati insoddisfacenti, poiché lo schema non ha la proprietà della positività e i processi iterativi spesso divergono. La stima della diffusione numerica introdotta dall'uso di schemi upwind su griglie simpliciali è un problema a sé stante. I lavori esistenti in questa direzione, che forniscono stime teoriche delle caratteristiche di convergenza, sono limitati a una varietà di schemi per il calcolo delle variabili nei centri delle celle. Pertanto, stimare il tasso di convergenza degli schemi MCO/FE sopravento utilizzando una serie di esperimenti numerici è di particolare importanza. Pertanto, la costruzione e l’analisi comparativa di schemi MCO/FE upwind su reti non strutturate è un argomento di ricerca attuale. L'obiettivo del lavoro è quello di sviluppare tecnologie computazionali per metodi ai volumi finiti che utilizzano spazi di elementi finiti per approssimare problemi di tipo convettivo-diffusionale. Per raggiungere questo obiettivo sono stati formulati i seguenti obiettivi di ricerca: 1) miglioramento delle tecnologie per discretizzare sistemi di leggi di conservazione utilizzando il metodo dei volumi finiti/elementi finiti su griglie simpliciali, utilizzando partizioni baricentriche come partizioni doppie; 2) sviluppo di tecnologie per l'approssimazione di problemi di tipo convettivo-diffusionale con derivate prime significative; costruzione, implementazione e analisi comparativa di schemi upstream su reti non strutturate, in particolare, conduzione di esperimenti computazionali per valutare l'ordine di approssimazione degli schemi proposti e più accurati conosciuti, nonché confronto delle caratteristiche degli schemi upstream basati su MCE/FE e FEM; 3) creazione, sulla base delle tecnologie sviluppate, di pacchetti software che consentano di simulare adeguatamente flussi viscosi incomprimibili di liquidi e gas in aree geometricamente complesse, in casi stazionari e non stazionari. Metodi di ricerca. Metodi di matematica computazionale. Analisi comparativa di tecnologie per l'esatta integrazione di polinomi in metodi agli elementi finiti, volumi/elementi finiti, residui distribuiti. Valutazione sperimentale della velocità di convergenza di schemi di flusso controvento per problemi con soluzione analitica. Calcoli su un insieme di partizioni di elementi finiti condensati, seguiti dall'analisi della convergenza ai dati sperimentali. La novità scientifica del lavoro è la seguente: 1. Viene proposta una nuova tecnologia per tenere conto della rappresentazione polinomiale a tratti della soluzione, dei coefficienti di trasferimento e dei termini sorgente durante la discretizzazione di problemi ai valori al contorno iniziale utilizzando i metodi dei volumi/elementi finiti, dei volumi finiti/elementi finiti e dei sottovolumi. La tecnologia si basa sull'uso dell'espansione di base degli spazi degli elementi finiti in termini di coordinate simpliciali baricentriche, con ulteriore esatta integrazione dei loro monomi. Per gli schemi MKO/FE, MKO/E con il calcolo delle variabili ai nodi di triangolazione, vengono proposte tre classi di formule per l'esatta integrazione dei monomi delle coordinate baricentriche: su segmenti della doppia mesh in un elemento, su sottoregioni e segmenti baricentrici dei bordi di confine. Per i metodi del sottovolume che utilizzano spazi di elementi finiti incoerenti, si propone di utilizzare il principio dell'esatta integrazione delle funzioni di base e si ottengono le corrispondenti formule integrali. 2. Viene proposto un metodo per costruire schemi MCO/FE sopravento su griglie semplici, basato sull'approssimazione separata dei flussi di massa e dei valori scalari delle sostanze su segmenti della doppia griglia. Vengono introdotti i concetti di matrice locale dei coefficienti di peso di uno schema controcorrente, interna agli elementi degli schemi, e di positività locale degli schemi. È stato proposto uno schema in controflusso di classe esponenziale, e il suo analogo è stato costruito per l'MKO con il calcolo dei simplessi sconosciuti nei baricentri. 3. Sono state ottenute stime sperimentali del tasso di convergenza dello schema controvento con pesatura dei flussi di massa e dello schema di classe esponenziale proposto. Utilizzando soluzioni del tipo strato limite, la stabilità degli schemi costruiti è stata analizzata e confrontata con gli schemi FEM a monte. 4. Utilizzando le tecnologie di approssimazione proposte per problemi di tipo convezione-diffusione, è stata creata una serie di programmi per modellare flussi viscosi incomprimibili in variabili naturali di velocità-pressione e sono stati condotti numerosi esperimenti computazionali confermando l'efficacia degli schemi costruiti. Struttura e ambito della tesi. La tesi è composta da un'introduzione, quattro capitoli, una conclusione, una bibliografia, un'appendice e contiene 173 pagine, comprese 10 tabelle e 51 figure. La bibliografia contiene 117 titoli.
Dissertazioni simili nella specialità "Modellazione matematica, metodi numerici e pacchetti software", 13.05.18 codice HAC
Metodo numerico per il calcolo dei flussi di gas viscoso comprimibile in un'ampia gamma di numeri di Mach 2004, Candidato di scienze fisiche e matematiche Chirkov, Denis Vladimirovich
Metodo per lo studio numerico del flusso attorno a configurazioni spaziali risolvendo le equazioni di Navier-Stokes basate su schemi di accuratezza di ordine elevato 2010, Dottore in scienze fisiche e matematiche Volkov, Andrey Viktorovich
Modellazione numerica del moto di un fluido viscoso incomprimibile a confini liberi utilizzando il metodo dei vicini naturali generalizzati 2008, Candidata di scienze fisiche e matematiche Rein, Tatyana Sergeevna
Sviluppo di una tecnologia di calcolo ad alta precisione basata sul metodo spettrale degli elementi finiti 2007, candidato di scienze fisiche e matematiche Poponin, Vladimir Sergeevich
Studio dei flussi di fluidi viscosi in canali di forma complessa 2002, candidato di scienze fisiche e matematiche Firsov, Dmitry Konstantinovich
Conclusione della tesi sul tema “Modellazione matematica, metodi numerici e pacchetti software”, Voitovich, Tatyana Viktorovna
Conclusione
Questo lavoro è dedicato allo sviluppo di tecnologie computazionali per metodi ai volumi finiti su griglie simpliciali, utilizzando spazi di elementi finiti e partizioni baricentriche come duali per approssimare problemi di tipo convettivo-diffuso! Il lavoro ha ottenuto i seguenti principali risultati per la difesa:
1. Viene proposta una nuova tecnologia per tenere conto della rappresentazione polinomiale a tratti della soluzione, dei coefficienti di trasferimento e dei termini sorgente durante la discretizzazione di problemi ai valori al contorno iniziale utilizzando i metodi dei volumi/elementi finiti, dei volumi finiti/elementi finiti e dei sottovolumi. La tecnologia si basa sull'uso dell'espansione di base degli spazi degli elementi finiti in termini di coordinate simpliciali baricentriche, con ulteriore esatta integrazione dei loro monomi. Per gli schemi MKO/FE, MKO/E con il calcolo delle variabili ai nodi di triangolazione, vengono proposte tre classi di formule per l'esatta integrazione dei monomi delle coordinate baricentriche: su segmenti della doppia mesh in un elemento, su sottoregioni e segmenti baricentrici dei bordi di confine. Per i metodi del sottovolume che utilizzano spazi di elementi finiti incoerenti, si propone di utilizzare il principio dell'esatta integrazione delle funzioni di base e si ottengono le corrispondenti formule integrali.
2. Viene proposto un metodo per costruire schemi MCO/FE sopravento su griglie semplici, basato sull'approssimazione separata dei flussi di massa e dei valori scalari delle sostanze su segmenti della doppia griglia. Vengono introdotti i concetti di matrice locale dei coefficienti di peso di uno schema a monte, interna agli elementi degli schemi, e di positività locale degli schemi. È stato proposto uno schema in controflusso di classe esponenziale, e il suo analogo è stato costruito per l'MKO con il calcolo dei simplessi sconosciuti nei baricentri.
3. Sono state ottenute stime sperimentali del tasso di convergenza dello schema controvento con pesatura dei flussi di massa e dello schema di classe esponenziale proposto. Utilizzando soluzioni del tipo strato limite, la stabilità degli schemi costruiti è stata analizzata e confrontata con gli schemi FEM a monte. È dimostrato che gli schemi MCO/FE completati consentono di tracciare le caratteristiche delle soluzioni dello strato limite in modo molto più accurato rispetto agli schemi del metodo Petrov-Galerkin con funzioni di base asimmetriche (polinomi di Legendre), schemi agli elementi finiti di Rice e Schnipke, così come schemi combinati di elementi finiti di un ordine di approssimazione superiore sviluppati da T. Sheu, S. Wang e S. Tsai.
4. Utilizzando gli schemi di approssimazione proposti per problemi di tipo convettivo-diffuso, è stato creato un insieme di programmi per modellare flussi viscosi incomprimibili in variabili naturali velocità-pressione, su griglie combinate, utilizzando polinomi di interpolazione di pressione e velocità dello stesso ordine; Sono stati condotti numerosi esperimenti computazionali per confermare l'efficacia dei circuiti costruiti.
5. Per un flusso di riferimento in un canale dietro un passaggio all'indietro, viene mostrata per la prima volta l'interazione tra l'effetto di input e l'effetto dell'utilizzo delle approssimazioni a monte.
Quindi, la tecnologia proposta nel lavoro per discretizzare i problemi dei valori al contorno iniziale utilizzando il metodo degli elementi finiti/volumi finiti su griglie simpliciali è un modo efficace per approssimare i sistemi di leggi di conservazione, gli schemi sviluppati controvento hanno buone caratteristiche di convergenza e l'uso di metodi di discretizzazione per un sistema di equazioni di Navier-Stokes con interpolazione dello stesso ordine per le componenti del vettore velocità-pressione consentono di ottenere risultati in buon accordo con i dati sperimentali. Classi di metodi a volumi finiti/elementi finiti su mesh semplici, la cui base tecnologica è l'esatta integrazione di monomi di coordinate baricentriche, sono metodi efficaci per modellare flussi viscosi incomprimibili in aree con geometria di confine complessa.
Elenco dei riferimenti per la ricerca della tesi Candidata di scienze fisiche e matematiche Voitovich, Tatyana Viktorovna, 2000
1. Belotserkovsky O.M., Modellazione numerica nella meccanica del continuo. M.: Scienza. Testa. ed. fisica e matematica letteratura, 1984.
2. A. S. Boldarev, V. A. Gasilov. O. G. Olkhovskaya, Verso la soluzione delle equazioni iperboliche su griglie non strutturate // Modellazione matematica. 1996. T. 8, n. 3. pp. 51-78.
3. P. A. Voinovich, D. M. Sharov, Modellazione di flussi di gas discontinui su griglie non strutturate // Modellazione matematica. 1993. T. 5. N. 7, pp. 86-114.
4. I. J1. Guryeva, Tecnologia computazionale del metodo dei volumi finiti // Dis. per il Candidato di Laurea in Scienze. f.-m. Sci. Novosibirsk 1997. - 115 pag.
5. Zhukov M.F., Solonenko O.P., Getti polverosi ad alta temperatura nella lavorazione di materiali in polvere. Novosibirsk IT SB RAS. 1990.
6. V. P. Ilyin, Schemi di differenza bilanciata di maggiore precisione su griglie rettangolari non uniformi. Novosibirsk 1994. - 31 pagine (Preprint/CC SB RAS n. 1031).
7. Ilyin V.P., Turakulov A.A., Sulle approssimazioni di equilibrio integro dei problemi dei valori al contorno tridimensionali. Novosibirsk, 1993. - 24 p. - (Prestampa/CC SB RAS: N. 986).
8. V. M. Kovenya, N. N. Yanenko, Metodo di scissione in problemi di dinamica dei gas. Novosibirsk, Scienza. 1989.
9. A. Ladyzhenskaya, Problemi matematici nella dinamica del fluido viscoso incomprimibile. M.: Tqc. casa editrice f.-m. lett.- 1961.
10. D. Oden, Elementi finiti nella meccanica del continuo non lineare. M.: Mir, 1976.
11. Patankar S., Metodi numerici per risolvere problemi di scambio termico e fluidodinamica. -M.:. Energoatomizdat, 1984.
12. N. Pissanetski S. Tecnologia delle matrici sparse. M.: Mir. 1988.
13. Preparata F. Sheimos M. Geometria computazionale; Introduzione. M." Mir, 1984.
14. A. A. Samarsky, Introduzione alla teoria degli schemi di differenza. M.: Nauka, 1971.
15. L Segerlind, Applicazione del metodo degli elementi finiti M.: Mir. 1979
16. N. K. Sukanek, R. P. Rhodes, Formulazione della condizione sull'asse di simmetria nel calcolo numerico dei flussi simmetrici // Rocketry and Cosmonautics, 1978. Vol. 16. No. 10). pp. 96-98.
17. R. Temam, equazioni di Navier-Stokes, teoria e analisi numerica // M.: Mir. 1981.
18. K. Fletcher, Metodi numerici basati sul metodo Galerkin II M.: Mir, 1991
19. D. Shi, Metodi numerici nei problemi di trasferimento di calore. M.; Mondo, 1988.
20. G. Schlichting, Teoria dello strato limite. M.: Casa editrice straniera. illuminato. 1956.
21. E. P. Shurina, T. V. Voitovich, Analisi di algoritmi per metodi agli elementi finiti e ai volumi finiti su mesh non strutturate durante la risoluzione delle equazioni di Navier-Stokes // Tecnologie computazionali. 1997. T. 2. N. 4. P. 84104.
22. E. P. Shurina, O. P. Solonenko, T. V. Voitovich, Nuova tecnologia del metodo dei volumi finiti su griglie simpliciali per problemi di tipo convettivo-diffusionale. Novosibirsk 1999. -51 e.- (Preprint/ ITAM SB RAS; N. 8-99).
23. I. Yu. Chumakov, "Uso di diverse condizioni per la pressione al confine di uscita nel calcolo dei flussi interni complessi di fluido incomprimibile su griglie combinate", Vestn. dicono scienziati. Ser. Matematica applicata e meccanica. 1997. T 1. P. 55-62.
24. N. N. Yanenko, Metodo dei passaggi frazionari per risolvere problemi multidimensionali di fisica matematica. Novosibirsk: Nauka, 1967.
25. Un primer agli elementi finiti. Agenzia nazionale per i metodi e gli standard degli elementi finiti //NEL. Glasgow, 1986.
26. K. Ajmani, WF Ng. SM. Leone, metodi di gradiente coniugati precondizionati per le equazioni di Navier-Stokes//J. Calcola. Fis. 1994.vol. 1 10. P. 68-81.
27. F. Angrand, A Dervieux, Alcuni schemi espliciti di elementi finiti triangolari per le equazioni di Eulero//Int. J.perNumero. Metodi nei fluidi. 1984.vol. 4. P.749-764.
28. P. Arminjon, A. Dervieux, Costruzione di viscosità artificiali TVD-Hke su griglie FEM arbitrarie bidimensionali // J. Comput. Fisica, 1993. vol. 106. P. 176-198.
29. B. Armaly, F. Durst, J. C. F. Pereira, B. Schoenung, Indagine sperimentale e teorica sul flusso a gradini rivolto all'indietro //J. Meccanismo fluido. 1983.vol. 127.473496.
30. F. Babuska, Limiti di errore per metodi agli elementi finiti//Numero. Matematica. 1971 Vol.16. P. 322-333.
31. Babuska, B. A. Szabo, I. N. Katz, La versione p del metodo degli elementi finiti // SIAM J. Numer. Anale. 1981.vol. 18. P. 516-544.
32. P. Balland, E. Suli, Analisi del metodo del volume finito cella-vertice per problemi iperbolici a coefficienti variabili // SIAM J. Numer. Anale. 1997.vol. 34. P. 1127-1151.
33. R. E. Bank, B. D. Welfert, Stime degli errori a posteriori per il problema di Stokes // SIAM J. Numer. Anale. 1991.vol. 28. P. 591-623.
34. T. J. Barth, D. C. Jespersen, The design and application of upwind plans on unstructured meshes // AIAA paper 89-0336.
35. E. Barton, Uno studio numerico del flusso su un gradino confinato rivolto all'indietro // Int. J.PerNumero. Metodi nei fluidi. 1995.vol. 21. P. 653-665.
36. E. Barton, L'effetto di ingresso del flusso laminare su una geometria del gradino rivolta all'indietro // Int. J.perNumero. Metodi nei fluidi. 1995.vol. 25. P. 633-644.
37. S. Benharbit, A. Chalabi, J. P Vila, Viscosità numerica e convergenza dei metodi ai volumi finiti per leggi di conservazione con condizioni al contorno // SIAM J. Nu-mer. Anale. 1995.vol. 32. P 775-796.
38. Z. Cai, Sul metodo degli elementi di volume finito //Numero. Matematica. 1991 vol. 58 P.713735.
39. Z. Cai, S. McCormick, Sulla precisione del metodo degli elementi di volume finito per equazioni di diffusione su griglie composite // SIAM J. Numer. Anale. 1990.vol. 27. P. 636-655.
40. Z. Cai, J. Mandel, S. McCormick, Il metodo degli elementi di volume finito per equazioni di diffusione su triangolazioni generali // SIAM J. Numer. Anale. 1991 Vol 28. P. 392402.
41. M. C. Ciccoli, Algoritmi di decomposizione del dominio adattivo e approssimazione di volumi finiti/elementi finiti per equazioni di advezione-diffusione // Journal of Scientific Computing. 1996. Vol 11. P 299-341.
42. P. Chatzipantelidis, Un metodo dei volumi finiti basato sull'elemento Crouzeix-Raviart per PDE ellittiche in due dimensioni //Numer. Math. 1999, Vol. 82. P. 409-432.
43. K. H. Chen, R H. Pletcher, Primitive variable- procedura di calcolo fortemente implicita per flussi viscosi a tutte le velocità // AIAA J. 1991. Vol. 29. P1241-1249.
44. S. Chou, D. Kwak, P. S. Vassilevski, Metodi misti a covolume per problemi ellittici su griglie triangolari // SIAM J. Numer. Anale. 1998.vol. 35. P. 1850-1861.
45. Christie, D. F. Griffiths, A. R. Mitchell e O. C. Zienkiewicz, Metodi degli elementi finiti per equazioni differenziali del secondo ordine con derivate prime significative // Int. J. Numero. Metodi L'Ing. 1976.vol. 10.1389-1396.
46. J.-P. Croisille, schemi a volume finito // Proc. del Secondo Stagista. Sintomo sui volumi finiti per applicazioni complesse, 19-22 luglio, 1999, Duisburg, Germania. Pubblicazioni scientifiche HERMES, Parigi, 1999.
47. V. Cockburn, F. Coquel. P. G. Lefloch, Convergenza del metodo dei volumi finiti per leggi di conservazione multidimensionali // SIAM J. Numer. Anale. 1995.vol. 32.687-705.
48. L. Davidson, Un metodo di correzione della pressione per mesh non strutturate con volumi di controllo arbitrari // Int. J. per Numero. Metodi nei fluidi. 1998.vol. 22. P. 265-281.
49. C. Debiez, A. Dervieux, K. Meg, B. Nkonga, Calcolo dei flussi instabili con metodi misti volume finito/elementi finiti controvento // Int. J. per Numero. Metodi nei fluidi. 1998.vol. 27. P. 193-206.
50. M. Delanaye, J. A. Essers, Schema di volume finito con ricostruzione quadratica per flussi comprimibili su griglie adattive non strutturate // AIAA Journal. 1997.vol. 35. P. 631-639.
51. Dervieux A., Simulazione Steady Euler utilizzando mesh non strutturate // Serie di conferenze VKI. 1985. N. 1884-04.
52. Eisenberg M. A., Malvern L. E., Sull'integrazione degli elementi finiti nelle coordinate naturali // Int. J. Numero. Metodi L'Ing. 1973.vol. 7.574-575.
53. A. Fezoui, Classe di schemi upwind impliciti per simulazioni di Eulero con maglie non strutturate//J. Sotr. Fis. 1989.vol. 84. P. 174-206.
54. C. Gallo, G. Manzini, Un approccio misto elementi finiti/volumi finiti per risolvere il trasporto di biodegradazione nelle acque sotterranee // Int. J. per Numero. Metodi nei fluidi.1998. vol. 26. P. 533-556.
55. T. Gallouet, J. P. Vila, Schemi a volumi finiti per leggi di conservazione di tipo misto // SIAM J. Numer. Anale. 1991.vol. 28. P. 1548-1573.
56. P. M. Gresho, S. T. Chan, R. L. Lee, G. D. Upson, Un metodo agli elementi finiti modificato per risolvere il problema dipendente dal tempo. Equazioni di Navier-Stokes incomprimibili. Parte 2: Applicazioni // Int. J. per Numero. Metodi nei fluidi, 1984. vol. 4. P.619640.
57. A. Grundmann, H. M. Moller, Formule di integrazione invariante per i-simplex mediante metodi combinatori // SIAM J. Numer. Anal 1978 vol. 15, pp. 282-290.
58. W. Hackbusch, Sugli schemi a scatola del primo e del secondo ordine // Informatica. 1989.vol. 41. P. 277-296.
59. L. P. Hackman, G. D. Raithby, A. B. Strong. Previsioni numeriche dei flussi su gradini rivolti all'indietro // Int. J. per Numero. Metodi nei fluidi. 1984.vol. 4. P.71 1-724.
60. L. Hallo, C. Ribault, M. Buffat, Un metodo implicito misto volume finito-elementi finiti per risolvere flussi comprimibili turbolenti 3D. J. per metodi numerici nei fluidi, 1997. vol. 25. P. 1241-1261.
61. F. H. Harlow, J. E. Welch, Calcolo numerico del flusso incomprimibile della viscosità dipendente dal tempo di fluido con superficie libera // Phys. Fluidi. 1965.vol. 8. P.21822189.
62. F. Ilinca, D. Pelletier, A. Garon, An Adaptive Finite Element Method for a Two-Equation turbulence Model in Wall-Bounded Flows. J. per Numero. Metodi nei fluidi. 1997.vol. 124. P 101-120.
63. E. Issman, G. Degrez, H. Deconinck, Implicit Upwind Residual-Distribution Euler e Navier-Stokes Solver on Unstructured Meshes // AIAA Journal, 1996. vol. 34. P.2021-2028.
64. J. P. Jessee, W. A. Fiveland, "Un algoritmo di vertici di cella per le equazioni di Navier-Stokes incomprimibili su griglie non ortogonali", Int. J. per Numero. Metodi nei fluidi. 1996.vol. 23. P. 271-293.
65. Jianguo H., Shitong X., Sul metodo degli elementi di volume finito per problemi ellittici autoaggiunti generali // SIAM .J Numer. Anale. 1998.vol. 35. P. 1762-1774.
66. M. Lallemand, H. Steve, A. Dervieux, Multigridding non strutturato per agglomerazione di volume: stato attuale // Computers Fluids, 1992 vol. 21. P. 397-433.
67. Y. Liu, M. Vinokur, Integrazione esatta di polinomi e formule di quadratura simmetrica su griglie poliedriche arbitrarie // J. Comput. Fis. 1998.vol. 140. P. 122-147.
68. D. Marcum, Modelli di turbolenza per calcoli agli elementi finiti non strutturati // Int. J.PerNumero. Metodi nei fluidi. 1995, vol. 20. P. 803-817.
69. C. Masson, H. I. Saabas, B. R. Baliga, Metodo degli elementi finiti del volume di controllo di ordine uguale co-locato per flusso di fluido incomprimibile assialsimmetrico bidimensionale // Int J. For Numer. Metodi nei fluidi. 1994.vol. 18. P. 1-26.
70. S. Mattiussi, Analisi dei finiti vol. Metodi agli elementi finiti e alle differenze finite che utilizzano alcuni concetti della topologia algebrica // J. Comput. Fis. 1997.vol. 133. P. 289-309.
71. D. Mavriplis, Soluzione multigriglia delle equazioni di Eulero bidimensionali su mesh triangolari non strutturate // AIAA Journal, 1988. Vol 26. P. 824-831.
72. P. R. McHugh, D. A. Knoll, "Soluzioni di volume finito completamente accoppiate dell'incomprimibile Navier-Stpkes ed equazioni dell'energia utilizzando un metodo di Newton inesatto", Int. J. Per numero. Metodi nei fluidi. 1994.vol. 19. P. 439-455.
73. Y. Murthy, S. Mathur, Flusso periodico e trasferimento di calore mediante reti strutturate // Int. J. per Numero. Metodi nei fluidi. 1997.vol. 25. P. 659-677.
74. S. Muzaferija, D. Gosman, Procedura CFD a volume finito e strategia di controllo adattivo degli errori di griglie di topologia arbitraria // J. Comput. Fisica, 1997, vol. 138. P. 766-787
75. P. Nithiarasu, O. C. Zienkiewlcz, V. V. K. Satya Sai, K. Morgan, R. Codina, M. Vazquez, Shock capturing viscosities for the general fluidomeccanica algoritmo // Int. J. per Numero. Metodi nei fluidi. 1998.vol. 28. P. 1325-1353.
76. K. Ohmori, T. Ushijima, Una tecnica di tipo upstream applicata ad un'approssimazione lineare non conforme agli elementi finiti delle equazioni di diffusione convettiva // R.A.I.R.O. Anale. Numero.
77. D. Pan, J. C. Cheng, Upwind finite volume Navier-Stokes Computations on Uns-structured Triangular Meshes // AIAA Journal, 1993. vol. 31. P. 1618-1625.
78. S. V. Potapov, Un algoritmo misto FE FV nella dinamica solida non lineare // Proc. del Secondo Stagista. Sintomo sui Volumi Finiti per Applicazioni Complesse. 19-22 luglio 1999. Duisburg, Germania. - Pubblicazioni scientifiche HERMES. Parigi. 1999. P. 271278.
79. C. Prakash, S. V. Patankar, Un metodo agli elementi finiti basato sul volume di controllo per risolvere le equazioni di Navier-Stokes utilizzando l'interpolazione velocità-pressione di ordine uguale //Numer. Trasferimento di calore. 1985.vol. 8. P. 259-280.
80. S. Ramadhyani, S. V. Patankar, Soluzione dell'equazione di Poisson: confronto tra il metodo Galerkin e quello del controllo del volume // Int. J. Numero. Metodi L'Ing. 1980.vol. 15.1395-1418.
81. Rida S., McKenty F., Meng F. L., Reggio M., Uno schema di controllo del volume sfalsato per griglie triangolari non strutturate // Int. J. per Numero. Metodi nei fluidi. 1995.vol. 25. P. 697-717.
82. P. L. Roe, solutori Riemann approssimati, vettori dei parametri e schemi di differenza //! Sotr. Fis. 1981.vol. 43. P. 357-372.
83. C. Rohde, Upwind Finite volume plans for debolmente accoppiati sistemi iperbolici di leggi di conservazione in 2D // Numer. Matematica. 1998.vol. 81. P. 85-123.
84. Tony W. H. Sheu, S. K. Wang, S. F. Tsai, Sviluppo di uno schema ad alta risoluzione per un'equazione di avvezione-diffusione multidimensionale // J. Sotr. Fis. 1998.vol. 144. P. 1-16.
85. Saad Y., Metodi iterativi per sistemi lineari sparsi. PSW Publishing Co., Boston, MA, 1995.
86. V. V. K. S. Sai, O. C. Zienkiewicz, M. T. Manzari, P. R. M. Lyra, K. Morgan, Scopo generale contro algoritmi speciali per flussi ad alta velocità con shock // Int. J. Numero. Meth. Fluidi. 1998.vol. 27. P. 57-80.
87. J. L. Sohn, Valutazione del FIDAP su alcuni benchmark classici laminari e turbolenti // Int. J. per Numero. Metodi nei fluidi. 1988.vol. 8. P. 1469-1490.
88. In Stoufflet, Investigation of generalized flux vector splitting for comprimible flow on triangular meshs // Int. J. per Numero. Metodi nei fluidi. 1995.vol. 20. P. 1047-1059.
89. B. Stouflette. J. Periaux, F. Fezoui, A. Dervieux, Simulazione numerica dei flussi di Eulero ipersonici 3-D attorno ai veicoli spaziali utilizzando elementi finiti adattati // Documento AIAA 87-0560.
90. C. Taylor, P. Hood, Una soluzione numerica delle equazioni di Navier-Stokes utilizzando la tecnica degli elementi finiti // Computer e fluidi. 1973.vol. 1. P. 73-100.
91. Thomadakis M, Leschziner M., Un metodo di correzione della pressione per la soluzione di flussi viscosi incomprimibili su griglie non strutturate // Int.J. per metodi numerici nei fluidi. -1996. vol. 22 P 581-601.
92. A. K. Verma, V. Eswaran, Approccio di controllo del volume sovrapposto per problemi di convezione-diffusione // Int. J. per Numero. Metodi nei fluidi. 1996.vol. 23. P. 865-882.
93. M. M. T. Wang, T. W. H. Sheu, Su un elemento finito compatto di ordine misto per risolvere le equazioni di Navier-Stokes incomprimibili tridimensionali // Int. J. per Numero. Metodi nei fluidi. 1997.vol. 25. P. 513-522.
94. M. M. T. Wang, T. W. H. Sheu, Implementazione di una condizione al contorno libera per le equazioni di Navier-Stokes // Int. J. Numero. Metodi Calore e flusso dei fluidi, 1997. Vol.7. P.95-111.
95. D. Winterscheidt, K. S. Surana, formulazione dei minimi quadrati della versione p per flussi di fluidi bidimensionali e incomprimibili // Int. J. Numero. Meth. Fluidi, 1994. vol. 18. P. 43-69.
96. A. M. Winslow, Soluzione numerica dell'equazione di Poisson quasilineare in una mesh triangolare non uniforme, J. Comput. Fis. 1967.vol. 2.149-172.
97. A. Younes, R. Mose. P. Ackerer. G. Chavent, Una nuova formulazione del metodo degli elementi finiti misti per risolvere PDE ellittiche e paraboliche con elementi triangolari // J. Comput. Fisica, 1999. vol. 149. P. 148-167.
98. P.J. Zwart, G. D. Raithby, M. J. Raw, Il metodo integrato dei volumi finiti spazio-temporali e la sua applicazione ai problemi dei confini in movimento // J. Comput. Fis. 1999.vol. 154. P. 497-519.
99. O. C. Zienkiewicz, Il metodo degli elementi finiti nelle scienze ingegneristiche // McGraw-Hill Londra. 1971.
100. OC Zienkiewicz, R. Codina, Un algoritmo generale per flusso comprimibile e incomprimibile. Parte 1: Lo schema suddiviso e basato sulle caratteristiche // Int. J. Numero. Meth. Fluidi. 1995.vol. 20. P. 869-885.
101. S. M. Rhie e W. L. Chow, Uno studio numerico del flusso turbolento oltre un profilo alare isolato con separazione del bordo d'uscita // Documento AIAA n. 82-0998. 1982.
102. R. I. Issa, Soluzione delle equazioni del flusso del fluido implicitamente discretizzate mediante suddivisione dell'operatore//J. Calcola. Fis. vol. 62. P. 40-65.1985.
103. J. Kim, S. J. Kline, J. P. Johnston, Investigation of a Reattatching Turbulent Shear Layer: Flow Over a Back-facing Step, Journal of Fluids Eng., vol. 102, pp. 302-308.117. http://www.ict.nsc.ru/linpar
Si prega di notare che i testi scientifici presentati sopra sono pubblicati solo a scopo informativo e sono stati ottenuti tramite il riconoscimento del testo della tesi originale (OCR). Pertanto, potrebbero contenere errori associati ad algoritmi di riconoscimento imperfetti. Non sono presenti errori di questo tipo nei file PDF delle tesi e degli abstract che consegniamo.
Qualche tempo fa stavo cercando una descrizione delle operazioni e dei processi che si verificano nella libreria di modellazione numerica OpenFOAM. Ho trovato molte descrizioni astratte del funzionamento del metodo dei volumi finiti, schemi di differenze classiche e varie equazioni fisiche. Volevo sapere più in dettaglio: da dove provengono questi valori in questo o quel file di output in questa o quella iterazione, quali espressioni si trovano dietro determinati parametri nei file di impostazioni fvSchemes, fvSolution?
Per coloro che sono interessati anche a questo, questo articolo. Coloro che conoscono bene OpenFOAM o i metodi in esso implementati scrivono degli errori e delle imprecisioni riscontrati in un messaggio personale.
C'erano già un paio di articoli su OpenFOAM su Habré:
Pertanto, non mi soffermerò sul fatto che si tratta di "una piattaforma aperta (GPL) per la simulazione numerica, progettata per simulazioni associate alla risoluzione di equazioni differenziali parziali utilizzando il metodo dei volumi finiti, ed è ampiamente utilizzata per risolvere problemi nella meccanica del continuo".
Oggi utilizzerò un semplice esempio per descrivere le operazioni che avvengono durante i calcoli in OpenFOAM.
Quindi, data la geometria, un cubo con un lato di 1 metro:
Ci troviamo di fronte al compito di modellare la propagazione del flusso di un certo campo scalare (temperatura, quantità di materia), che è dato dalla seguente equazione di trasporto (1) all'interno del volume del corpo.
(1) ![]() ,
,
Dove una quantità scalare, ad esempio, esprime la temperatura [K] o la concentrazione di una determinata sostanza, ed esprime il trasferimento di una sostanza, il flusso di massa [kg/s].
Questa equazione viene utilizzata, ad esempio, per modellare la propagazione del calore ![]() ,
,
dove k è la conduttività termica e la temperatura [K].
L'operatore di divergenza è in realtà
operatore.
Lascia che ti ricordi che esiste un operatore nabla (operatore Hamilton), che è scritto come segue: ![]() ,
,
Dove i, j, k sono vettori unitari.
Se moltiplichiamo scalarmente l'operatore nabla per una quantità vettoriale, otteniamo la divergenza di questo vettore:
“Dal punto di vista della fisica, la divergenza di un campo vettoriale è un indicatore della misura in cui un dato punto nello spazio è sorgente o pozzo di questo campo”
Se moltiplichi l'operatore nabla per uno scalare, ottieni il gradiente di quello scalare:
Un gradiente mostra un aumento o una diminuzione in una certa direzione della grandezza di uno scalare.
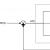
Le condizioni al contorno del problema sono le seguenti: c'è una faccia di ingresso, una faccia di uscita e le restanti facce sono pareti lisce.

Dividere il volume di un cubo in volumi finiti
La nostra griglia sarà molto semplice: dividiamo il cubo in 5 celle uguali lungo l'asse Z.
Tante formule
Il metodo dei volumi finiti prevede che (1) in forma integrale (2) sarà soddisfatto per ogni volume finito.
(2)![]() ,
,
Dov'è il centro geometrico del volume finale.
Centro del volume finale

Semplifichiamo e trasformiamo il primo termine dell'espressione (2) come segue:
(2.1) (HJ-3.12)*
Come puoi vedere, abbiamo assunto che la quantità scalare cambi linearmente all'interno del volume finito e il valore della quantità in un punto all'interno del volume finito può essere calcolato come:
Per semplificare il secondo termine dell'espressione (2), utilizziamo il teorema generalizzato di Gauss-Ostrogradsky: l'integrale della divergenza del campo vettoriale sul volume è uguale al flusso vettoriale attraverso la superficie che delimita il volume dato. Nel linguaggio umano, “la somma di tutti i flussi dentro/da un volume finito è uguale alla somma dei flussi attraverso le facce di questo volume finito”:
(2.3)![]() ,
,
Dov'è la superficie chiusa che limita il volume,
- vettore diretto lungo la normale al volume.
vettore s

Considerando che il volume finito è limitato da un insieme di facce piane, l’espressione (2.3) può essere trasformata nella somma degli integrali sulla superficie:
(2.4) (HJ-3.13)
,
Dove esprime il valore della variabile al centro della faccia,
- vettore d'area, uscente dal centro della faccia, diretto lontano dalla cellula (localmente), lontano dalla cellula con indice più basso verso la cella con indice più alto (globale).
Qualcosa in più sul vettore S
Per non memorizzare due volte gli stessi parametri vettoriali, perché È ovvio che per due celle vicine, il vettore normale al bordo tra le celle, diretto lontano dal centro della cella, differirà solo nel segno di direzione. Pertanto, è stata creata una relazione proprietario-vicino tra il bordo e la cella. Se il vettore dell'area (direzione globale e positiva da una cella con un indice inferiore a una cella con un indice maggiore) indica DAL centro della cella, tale relazione tra la cella e il vettore, e più precisamente tra la cella e il volto, è indicato come proprietario). Se questo vettore punta all'interno della cella in questione, allora il vicino. La direzione influenza il segno del valore (+ per il proprietario e - per il vicino) e questo è importante quando si somma, vedi sotto.
A proposito di schemi di differenza
Il valore al centro del viso viene calcolato attraverso i valori al centro delle celle adiacenti: questo metodo di espressione è chiamato schema di differenza. In OpenFOAM, il tipo di schema di differenza è specificato nel file /system/fvSchemes:DivSchemes ( predefinito nessuno; div(phi,psi) Gauss lineare; )
Gauss- significa che è selezionato lo schema della differenza centrale;
lineare- significa che l'interpolazione dai centri delle celle ai centri delle facce avverrà in modo lineare.

Supponiamo che la nostra quantità scalare cambi linearmente all'interno del volume finito dal centro verso i bordi. Successivamente verrà calcolato il valore approssimato al centro del viso secondo la formula:
Dove sono i pesi e vengono calcolati come
Dove sono i volumi delle celle.
Per i casi di celle inclinate, esistono formule più complesse per il calcolo dei pesi di approssimazione.
Pertanto, i valori phi_f ai centri dei bordi delle celle vengono calcolati in base ai valori ai centri delle celle. I valori del gradiente grad(phi) vengono calcolati in base ai valori phi_f.
E l'intero algoritmo può essere rappresentato sotto forma del seguente pseudocodice.
1. Dichiariamo un array di gradienti di volumi finiti, inizializziamolo con zeri 2. Esaminiamo tutte le facce interne (che non sono confine) > Calcoliamo flusso_f = phi_f*S_f. Calcola i valori phi_f in base ai valori phi in centesimi di cella > Aggiungi flux_f al gradiente dell'elemento proprietario e -flux_f al gradiente dell'elemento vicino 3. Itera su tutte le facce di confine > Calcola flux_f = phi_f*S_f > Aggiungi flux_f al gradiente dell'elemento proprietario (vicino: le facce di confine non hanno elementi) 4. Esaminiamo tutti gli elementi > Dividi la somma del gradiente risultante per il volume dell'elemento
Campionamento temporale

Tenendo conto della (2.1) e della (2.4), l'espressione (2) assume la forma:
(3)
Secondo il metodo dei volumi finiti, viene effettuata la discretizzazione temporale e l'espressione (3) viene scritta come:
(4)
Integriamo (4):
(4.1)![]()
Dividiamo i lati sinistro e destro in:
(5)
Dati per la matrice di campionamento
Ora possiamo ottenere un sistema di equazioni lineari per ogni volume finito.Di seguito la numerazione dei nodi della griglia che utilizzeremo. 
Le coordinate dei nodi sono memorizzate in /constant/polyMesh/points
24
((0 0 0)
(1 0 0)
(0 1 0)
(1 1 0)
(0 0 0.2)
(1 0 0.2)
(0 1 0.2)
(1 1 0.2)
(0 0 0.4)
(1 0 0.4)
(0 1 0.4)
(1 1 0.4)
(0 0 0.6)
(1 0 0.6)
(0 1 0.6)
(1 1 0.6)
(0 0 0.8)
(1 0 0.8)
(0 1 0.8)
(1 1 0.8)
(0 0 1)
(1 0 1)
(0 1 1)
(1 1 1))
Numerazione dei centri dei nodi delle celle (50, 51 - centri delle facce di confine): 
Numerazione dei nodi centrali della faccia: 
Volumi degli elementi:
Coefficienti di interpolazione necessari per calcolare i valori sulle facce delle celle. Il pedice "e" indica il "bordo destro della cella". A destra rispetto alla vista, come nella figura “Numerazione dei nodi-centri delle celle”:
Formazione della matrice di campionamento
Per P = 0.
Espressione (5) che descrive il comportamento della quantità

Verrà trasformato in un sistema di equazioni algebriche lineari, ciascuna della forma:
Oppure, secondo gli indici dei punti sulle facce
E tutti i flussi da/verso una cella possono essere espressi come somma

Dove, ad esempio, è il coefficiente di linearizzazione del flusso nel punto centrale della cella E,
- coefficiente di linearizzazione del flusso nel punto centrale della faccia,
- parte non lineare (ad esempio costante).
A seconda della numerazione dei volti l'espressione assumerà la forma: 
Tenendo conto delle condizioni al contorno per l'elemento P_0, l'equazione algebrica lineare può essere rappresentata come
...sostituire i coefficienti ottenuti in precedenza...

Il flusso proveniente dall'ingresso"a è diretto nella cella e quindi ha segno negativo.
Poiché nella nostra espressione di controllo abbiamo anche, oltre al termine di diffusione, un termine temporale, ma l'equazione finale assomiglia
Per P = 1.
Per P = 4.
Un sistema di equazioni algebriche lineari (SLAE) può essere rappresentato in forma matriciale come
A(i,j) === 40,5 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40,5
Psi = dimensioni; InternalField Elenco non uniforme
In base al quale si ottengono i valori per il vettore
Quindi il vettore viene sostituito nello SLAE e avviene una nuova iterazione del calcolo del vettore.
E così via fino a quando la discrepanza raggiunge i limiti richiesti.