Construcción de mallas para el método de volúmenes finitos. Método de volúmenes finitos. Dividir el volumen de un cubo en volúmenes finitos
La ventaja de este método es que se basa en leyes de conservación. Por lo tanto, a diferencia del método de diferencias finitas, el método del volumen de control garantiza la conservación del esquema numérico, lo que permite obtener soluciones aceptables en términos de precisión incluso en cuadrículas relativamente gruesas.
La idea principal del método es bastante simple y fácilmente susceptible de interpretación física. Al discretizar las ecuaciones de Navier-Stokes promediadas por Reynolds, el dominio computacional se divide en una gran cantidad de volúmenes elementales que no se superponen, de modo que cada volumen contiene solo un punto computacional (nodal). El conjunto de volúmenes elementales se denomina malla computacional. Las celdas de la cuadrícula pueden tener diferentes formas. Los más utilizados son los hexaedros (hexaedros) y los tetraedros (tetraedros). El método del volumen de control permite el uso de celdas con un número arbitrario de caras (pirámides, prismas, poliedros complejos, etc.).
La solución al sistema de ecuaciones (1) a (18) se representa como un conjunto de valores de los parámetros deseados en los centros de estos volúmenes. Por ejemplo, si dividimos el volumen de una habitación en 1000 volúmenes elementales individuales (celdas), como resultado de la solución tendremos 1000 valores de temperatura, velocidad, presión, etc. La Figura 2 muestra un fragmento del dominio computacional. Las celdas están numeradas con índices. yo, j, k.
Arroz. 2. Fragmento del dominio computacional
La integración de ecuaciones diferenciales se realiza sobre cada volumen elemental. Las integrales se calculan mediante fórmulas de interpolación, que se utilizan para determinar los valores de las variables deseadas entre los puntos calculados. Como resultado, se obtiene un análogo discreto de las ecuaciones originales en puntos nodales, que refleja la ley de conservación de las variables estudiadas en cada volumen finito.
Cabe señalar que en la mayoría de los paquetes hidrodinámicos computacionales modernos, como "STAR-CD", "FLUENT", "CFX" y muchos otros, se implementa el método del volumen de control para discretizar las ecuaciones del modelo.
Cuadrículas de cálculo
El proceso de construcción de una malla es uno de los momentos clave en la realización de un experimento numérico. Seleccionar y construir una cuadrícula computacional adecuada para el problema bajo consideración es un procedimiento bastante complejo y que requiere mucho tiempo. Una elección racional de la malla puede simplificar significativamente la solución numérica del problema.

Arroz. 3. Configuraciones de celdas de cuadrícula
Las celdas de la cuadrícula pueden tener diferentes formas (Fig. 3) y tamaños que mejor se adapten a la solución de un problema específico. El tipo de cuadrícula más simple es cuando las celdas son idénticas y tienen forma cúbica.
Como regla general, cerca de superficies sólidas la malla se vuelve más densa, es decir, las células tienen un tamaño más pequeño normal a la superficie. Esto se hace para mejorar la precisión de los cálculos en aquellas áreas donde los gradientes de flujo de los parámetros estudiados cambian más rápidamente, por ejemplo, en la capa límite.
Puede aumentar la precisión de los cálculos y reducir el error de aproximación de dos formas:
· aumentar el orden de precisión del muestreo;
· disminuir el paso de la cuadrícula.
Al resolver problemas no estacionarios, los tamaños de celda Δx y el paso de integración temporal Δt están relacionados con la condición CFL (Courant-Friedrichs-Levy):  , tu- velocidad.
, tu- velocidad.
Los programas informáticos universales que se utilizan actualmente en la práctica de la ingeniería permiten trabajar en mallas arbitrarias no estructuradas utilizando elementos muy sesgados. En este caso, el orden de precisión de la discretización, por regla general, no excede el segundo. Para obtener una solución de alta calidad, es necesario construir grillas computacionales con pequeños pasos.
El paquete STAR-CCM ha cambiado al uso de células poliédricas (similares a un balón de fútbol), que, al combinar células, elimina la apariencia de células muy sesgadas.
La principal ventaja de las mallas no estructuradas en comparación con las regulares es una mayor flexibilidad para discretizar una región física de forma compleja. En este caso, las celdas de la cuadrícula deben tener volúmenes o áreas comparables y no deben cruzarse. Sin embargo, las desventajas de este tipo de malla incluyen un aumento en la dimensión de la malla. Como muestra la práctica, para el mismo objeto, una malla no estructurada, cuando se construye correctamente, tiene aproximadamente el doble de celdas que una estructurada, lo que naturalmente conduce a un aumento en el tiempo de cálculo en relación con las mallas regulares. Sin embargo, en muchos casos, las mallas no estructuradas son la única opción de construcción posible debido a la complejidad de la geometría del objeto. Además, con una elección racional del algoritmo de mallado, el tiempo dedicado a construir una malla no estructurada resulta ser significativamente menor que el tiempo necesario para construir una malla estructurada (estructurada en bloques). Como resultado, el tiempo total dedicado a resolver el problema (incluido el tiempo de mallado y el tiempo de cálculo) puede ser mucho menor cuando se utilizan mallas no estructuradas que en el caso de mallas estructuradas.
Determinar el tamaño de malla requerido es, en sí mismo, una tarea muy difícil. El método universal que se debe seguir al elegir la dimensión de la cuadrícula se reduce al hecho de que la solución resultante no debe cambiar cuando aumenta el número de celdas (convergencia de la cuadrícula).
Para problemas típicos, no es necesario realizar un estudio de convergencia de red, ya que se puede confiar en los resultados obtenidos previamente. Cuando se pasa a estudiar un nuevo tipo de problema, es imperativo realizar un estudio de convergencia de la red y determinar los requisitos para la red computacional.
Tenga en cuenta que al resolver problemas reales de ventilación y aire acondicionado, el número característico de celdas es, por regla general, de 500 mil a 3-4 millones, dependiendo de la complejidad geométrica del objeto, el conjunto de parámetros requeridos y las características específicas de el problema. En este caso, el tiempo de cálculo en un clúster que consta, por ejemplo, de 24 núcleos, puede alcanzar hasta una semana, y al resolver problemas no estacionarios, hasta varias semanas.
El paquete STAR-CCM+ incluye un módulo para crear mallas computacionales. También existen paquetes separados para generar mallas, por ejemplo, el más utilizado es ANSYS, ICEM CFD (ICEM). Las mallas integradas en paquetes externos se pueden importar al paquete STAR-CCM+.
Capítulo 1. Métodos de discretización de sistemas de leyes de conservación.
1.1. Principios tecnológicos de los métodos de discretización para problemas de valores en la frontera inicial utilizando espacios de elementos finitos.
1.1.1. Métodos de elementos finitos.
1.1.2. Métodos de volúmenes finitos.
1.2. Esquemas de ceñida sobre cuadrículas simples.
1.3. Métodos para resolver el sistema estacionario de ecuaciones de Navier-Stokes.
Capítulo 2. Construcción de análogos discretos de ecuaciones de reacción de difusión-convectiva utilizando el método de volumen finito
2.1. Discretización MKO/FE de problemas de tipo convectivo-difusión.
2.1.1. Triangulación y método para construir una malla dual.
2.1.2. Forma integral de leyes de conservación.
2.1.3. Aproximación de flujos de difusión y cálculo de la matriz de rigidez MKO/FE.
2.1.4. Aproximación de los términos fuente.
2.1.5. Cálculo de la matriz de masas MCO/FE.
2.1.6. Contabilización de las condiciones de contorno.
2.2. Construcción de esquemas multidimensionales a barlovento sobre grillas simpliciales.
2.2.1. Cálculo de matrices locales convectivas.
2.2.2. Esquemas con pesaje de flujos másicos.
2.2.3. Modificación de esquemas exponenciales.
2.2.4. Algunas propiedades de los esquemas de contraflujo y principios de su construcción.
2.2.5. Un análogo del esquema exponencial para esquemas con cálculo de incógnitas en los centros de celdas.
2.3. Nuevas clases de fórmulas integrales MKO.
2.3.1. Integración de monomios de coordenadas baricéntricas.
2.3.2. Sobre posibles combinaciones de representaciones polinómicas.
2.3.3. Sobre el aumento del orden de los polinomios de interpolación de la representación de la solución local.
2.4.4. Uso de elementos finitos inconsistentes.
2.4. Ensamblaje por elementos de matrices globales.
Capítulo 3. Modelado del campo de flujo de medios viscosos incompresibles.
3.1. Modelo matemático.
3.2. Forma integral de leyes de conservación.
3.3. Teniendo en cuenta la relación entre los campos de velocidad y presión.
3.3.1. Interpolación de Ry-Chow para calcular flujos de masa.
3.3.2. Discretización de la ecuación de continuidad.
3.3.3. Contabilización de límites con flujo másico distinto de cero.
3.3.4. Esquema general de iteración 1.
3.4. Acelerar la convergencia de esquemas iterativos.
3.4.1. Corrección de campos de presión y velocidad.
3.4.2. Esquema general de iteración II.
3.5. Resolución de sistemas de ecuaciones algebraicas lineales.
Capítulo 4. Experimentos numéricos.
4.1. Análisis de estabilidad para soluciones tipo capa límite.
4.2. Aceleración del flujo en una tubería redonda.
4.3. Flujo en el tramo inicial de un canal liso.
4.4. Flujo laminar de un chorro desde una boquilla puntual (chorro fuente)
4.5. Flujo laminar detrás de un escalón plano asimétrico.
4.5.1. Cálculo utilizando varios esquemas upstream.
4.5.2. Efecto de entrada al calcular flujos detrás de un paso hacia atrás usando MKO/FE en grillas simpliciales.
4.5.3. Comparación de diferentes métodos de resolución de sistemas de ecuaciones algebraicas lineales.
Lista recomendada de disertaciones.
Modelado de flujos internos de un fluido viscoso incompresible por el método de elementos finitos utilizando esquemas de contraflujo. 2007, Candidata de Ciencias Físicas y Matemáticas Gobysh, Albina Vladimirovna
Esquemas numéricos basados en aproximaciones de volumen finito/elementos finitos para resolver problemas de hidrodinámica de onda larga 2004, candidato de ciencias físicas y matemáticas Styvrin, Andrey Vadimovich
Tecnologías paralelas para resolver problemas de valores límite. 2005, Doctor en Ciencias Físicas y Matemáticas Vasilevsky, Yuri Viktorovich
Método de volúmenes finitos para problemas de convección-difusión y modelos de flujo bifásico. 2010, Candidato de Ciencias Físicas y Matemáticas Nikitin, Kirill Dmitrievich
Modelado tridimensional de procesos de transferencia de impurezas en medios porosos de estructura compleja. 2007, Candidato de Ciencias Físicas y Matemáticas Kapyrin, Ivan Viktorovich
Introducción de la tesis (parte del resumen) sobre el tema “Tecnologías del método de volumen finito/elementos finitos sobre rejillas simpliciales para problemas de tipo convectivo-difusión”
La solución numérica de problemas de física matemática es uno de los principales métodos para estudiar fenómenos reales. El uso combinado de experimentos físicos y computacionales en el análisis de cualquier fenómeno permite, por un lado, reducir el número de costosas mediciones experimentales y, por otro, verificar y mejorar los modelos matemáticos.
A medida que aumenta la velocidad de los sistemas informáticos, surgen nuevas demandas sobre los métodos numéricos para resolver problemas de física matemática. El desarrollo y mejora de métodos modernos para discretizar las leyes de conservación, que brindan la capacidad de simular clases de problemas siempre nuevos y obtener resultados significativamente mejores al resolver los conocidos, es un área importante de investigación.
Los algoritmos computacionales modernos deberían proporcionar la descripción más precisa de áreas con geometría compleja. Esto es posible utilizando mallas no ortogonales y no estructuradas. En comparación con las mallas arbitrarias no ortogonales, para las mallas simpliciales no estructuradas (triangulación en el caso bidimensional y partición en tetraedros en el caso tridimensional), las condensaciones locales son más fáciles de implementar (por ejemplo, detrás de un escalón trasero, en una zona de estrechamiento repentino, en las proximidades del punto de unión), y también, si es necesario, adaptación de la cuadrícula computacional en función del comportamiento de la solución. Por lo tanto, incluso cuando se discretizan leyes de conservación en dominios geométricamente simples que pueden representarse con precisión mediante una colección de elementos rectangulares, las mallas simpliciales no estructuradas tienen una serie de ventajas. A pesar de las ventajas obvias de las cuadrículas no estructuradas para aproximar regiones arbitrarias y la posibilidad de construir automáticamente particiones simpliciales, prácticamente no se han utilizado en dinámica de fluidos computacional y solo en los últimos 15 años se han vuelto cada vez más populares. Según B. Stoufflett et al., la razón de esto es el rápido aumento del tiempo de cálculo al pasar a enfoques no estructurados. El hecho es que la posición de los elementos distintos de cero en las matrices de análogos discretos depende de la contigüidad de los nodos de la cuadrícula y, de manera arbitraria, las matrices se almacenan utilizando formatos y estructuras de datos universales. Las operaciones de multiplicar una matriz dispersa por un vector y la factorización incompleta se vuelven mucho más "caras". Al mismo tiempo, los sistemas de ecuaciones de dinámica de fluidos computacional son sistemas de ecuaciones no lineales interconectados, cuyos esquemas de solución implícitos tienen una naturaleza iterativa de múltiples niveles, de modo que en cada una de las iteraciones "globales" es necesario resolver varios sistemas de ecuaciones algebraicas lineales. Fue con la llegada de potentes sistemas informáticos, así como gracias al desarrollo de métodos adaptativos y multirredes, que fue posible utilizar redes no estructuradas y los correspondientes esquemas de discretización espacial para modelar procesos hidrogasdinámicos.
El método de discretización más común en el caso no estructurado es el método de elementos finitos (FEM). Observemos ventajas del método como la preservación de la naturaleza simétrica de la parte autoadjunta de los operadores diferenciales en sus análogos discretos (esto se logra mediante una elección especial del espacio de funciones de prueba que coincide con el espacio de funciones de prueba) , la posibilidad de aumentar la precisión de la aproximación aumentando el grado de interpolación de los polinomios de la representación de la solución local (las llamadas versiones p y h-p de FEM, ), consideración natural de las condiciones de contorno del segundo y tercer tipo. El método de los elementos finitos tiene una base tecnológica establecida, en particular
Métodos para aproximar productos internos bajo el supuesto de una representación polinómica por partes de la solución y parámetros de un problema de valores en la frontera, a saber: el uso de la expansión de bases del correspondiente espacio de elementos finitos, clases de fórmulas integrales que permiten una integración precisa de productos arbitrarios de funciones de base sobre elementos de partición y bordes (caras) de elementos,
Aparato de interpolación estándar.
Las tecnologías del método permiten construir de manera simple y uniforme análogos discretos de problemas de valores de frontera iniciales, con varios tipos de condiciones de frontera bajo el supuesto de un cierto grado de suavidad de la solución y un comportamiento polinomial por partes de los coeficientes de las ecuaciones y condiciones de borde , .
En una serie de aplicaciones, como el modelado de flujos de gas supersónicos y transónicos y los cálculos utilizando modelos de aguas poco profundas, el conservadurismo local de los esquemas utilizados para discretizar las leyes de conservación es muy importante. El método de los elementos finitos no permite rastrear con precisión satisfactoria las características de las soluciones discontinuas emergentes, y el enfoque tradicional para resolver tales problemas es el método del volumen finito. Al discretizar un sistema de leyes de conservación por el método de volúmenes finitos, el dominio computacional se aproxima mediante un conjunto de volúmenes finitos abiertos, luego el investigador da un “paso atrás”, pasando a la forma integral del sistema de ecuaciones original; Usando la fórmula de Ostrogradsky-Gauss, pasamos de la integración de volumen a la integral de frontera, de modo que el método de aproximación de flujos a través de las caras de volúmenes finitos determina completamente el esquema computacional. Según la monografía de S. Patankar, "para la mayoría de los investigadores que trabajan en el campo de la hidrodinámica y la transferencia de calor, el método de los elementos finitos todavía parece envuelto en un misterio. La formulación variacional e incluso el método de Galerkin no se prestan a una interpretación física simple". Al mismo tiempo, los esquemas de volúmenes finitos tienen un cierto significado físico del equilibrio de flujos y términos fuente en cada uno de los volúmenes finitos que se aproximan al dominio computacional, lo que hace que el método de volúmenes finitos sea más atractivo. La "simplicidad" de MKO es una de las razones de la falta de una base tecnológica general para el método.
Así, las ventajas de la versión clásica del MKO (método de volúmenes finitos/diferencias finitas, FVDM) incluyen el conservadurismo local de los esquemas discretos, una mayor simplicidad y claridad, y la posibilidad de tener en cuenta de forma natural las condiciones de contorno del segundo tipo. Además, en el caso de resolver problemas con predominio de la convección, se simplifica la implementación de esquemas de contraflujo, ya que se analizan y aproximan los flujos por las caras de volúmenes finitos.
Los intentos de sistematizar aproximaciones de volúmenes finitos llevaron a una combinación parcial de tecnologías FEM y el principio de integración sobre volúmenes finitos; Los primeros de ellos se remontan al trabajo de B. R. Baliga, K. Prakash y S. Patankar y se conocen como métodos CVFEM (métodos de elementos finitos basados en volumen de control), en adelante denominados métodos de volumen finito/elementos finitos (FVM/ FE). Los autores del método persiguieron el objetivo de construir esquemas conservadores del método de volúmenes finitos, utilizando una de las principales ventajas del MEF: la capacidad de aproximar geometrías complejas utilizando mallas no estructuradas. Las funciones de perfil en esta clase de métodos son “de naturaleza auxiliar”, no se enfatiza la pertenencia de la solución a espacios de elementos finitos. Los conjuntos baricéntricos se utilizan como partición dual.
Por primera vez, el problema de la falta de principios tecnológicos universales del método de volúmenes finitos/diferencias finitas (MKO/KR, FVDM) se analiza en el trabajo de Z. Kaya “Sobre el método de volúmenes finitos/elementos”. El autor llama la atención del lector sobre la "naturaleza no sistemática del método del volumen finito/diferencias finitas"; Al aproximar sistemas de leyes de conservación mediante el método de volumen finito/diferencias finitas, se pueden utilizar aproximaciones de diferentes clases dentro de un mismo trabajo, lo que complica significativamente el análisis de la convergencia de tales esquemas. Se propone una solución a este problema: el uso conjunto de las ideas del método de los elementos finitos (buscar una solución en algún espacio de elementos finitos y utilizar el comportamiento polinómico por partes de la solución para calcular los flujos) y la forma integral de las leyes de conservación. Así, los métodos de volumen/elemento finito (FME/E, “métodos de caja”, FVE) surgieron en un intento de crear “tecnologías de volumen finito más sistemáticas”. La ausencia de principios tecnológicos generales de los métodos de volumen finito/diferencias finitas también se observa en los trabajos de Ya.JI. Guryeva y V. P. Ilyin.
Los métodos de volumen finito/elementos finitos (FVE) y los métodos de volumen finito/elementos finitos (CVFEM) utilizan espacios de elementos finitos consistentes de funciones lineales en símplex y pertenecen a la clase de esquemas de volumen finito de vértice de celda, Fig. 1, a.
Varios esquemas de dinámica de fluidos computacional (modelado de flujos viscosos e incompresibles) utilizan espacios de elementos finitos inconsistentes, en particular, el espacio de Crousey-Raviard lineal sobre elementos continuos en los centros de los bordes de las funciones de prueba. Los métodos de volumen finito que utilizan espacios de elementos finitos inconsistentes fueron propuestos por S. Choi y D. Kwak, estudiados en varios trabajos de otros autores (los llamados métodos de subvolumen, método de covolumen) y son esquemas con el cálculo de incógnitas en los centros. de bordes ( Los esquemas más comunes para resolver problemas de dinámica de gases y modelar desastres antropogénicos utilizando ecuaciones de aguas poco profundas son los esquemas de volumen finito centrados en celdas, Fig. 1, f. Su popularidad se debe al hecho de que en el caso del cálculo de incógnitas en los centroides, la mayoría de los esquemas de dinámica de gases (esquemas de S.K. Godunov, esquemas TVD) pueden transferirse a redes no estructuradas sin cambios tecnológicos fundamentales. o un en Figura 1. Ubicación de los puntos de cálculo en relación con los nodos de la cuadrícula FE. Este trabajo considera principalmente clases de métodos de volúmenes finitos con el cálculo de incógnitas en nodos de triangulación (MKO/E, MKO/FE) y centros de borde (métodos de subvolumen); en el futuro también diremos "métodos de volúmenes finitos que utilizan espacios de elementos finitos". " Estas clases de métodos, según varios estudios (, ), para problemas de convección-difusión proporcionan mejores aproximaciones a la solución que los métodos con cálculo de incógnitas en los centros de las celdas. Una de las razones principales es que para los métodos enumerados anteriormente, se preserva la continuidad de las primeras derivadas de las funciones de prueba en los elementos de la malla dual. Un enfoque eficaz para resolver problemas con predominio de convección es el uso del método Galerkin con funciones de prueba simétricas para la parte autoadjunta de los operadores diferenciales y esquemas MCO ascendentes para su parte asimétrica, la llamada. Métodos mixtos de elementos finitos/volumen (FEM/O, MEV, método mixto de elementos/volumen). El trabajo de tesis está dedicado, en particular, a mejorar las tecnologías del método de volúmenes finitos para las clases de métodos indicadas (MKO/E, MKO/CE, FEM/O, métodos de subvolumen). Por el momento, estos métodos no cuentan con tecnologías establecidas para tener en cuenta el comportamiento polinómico por partes de la solución, los términos fuente y los coeficientes de transferencia. Podemos enumerar las siguientes razones de la imperfección del aparato para la integración exacta de polinomios en métodos de volúmenes finitos utilizando espacios de elementos finitos: 1. A diferencia del método de elementos finitos, el método de volúmenes finitos no tiene una versión p, ya que con la introducción de nodos adicionales y varios tipos de mallas duales, el conservadurismo local de una serie de variables del sistema de leyes de conservación en relación a volúmenes finitos “ajenos” se viola. Por tanto, las aproximaciones se limitan a espacios de elementos finitos de orden inferior. 2. En comparación con el método de elementos finitos, los métodos de volúmenes finitos se caracterizan por una mayor libertad en la elección de los espacios de las funciones de prueba, que en este caso resultan estar relacionados con la ubicación de los puntos de cálculo de las incógnitas en relación con la discretización. nodos (esquemas con la ubicación de las incógnitas en nodos, puntos medios de aristas, centroides simples) y el método de construcción de una cuadrícula dual (usando conjuntos baricéntricos, ortocéntricos y circuncéntricos). Combinado con la capacidad de utilizar cuadrículas colocadas o escalonadas, esto brinda la variedad completa de esquemas MCM existentes en cada aplicación. Para los métodos MCM para discretizar leyes de conservación que utilizan espacios de elementos finitos, una selección cuidadosa de estos espacios para la solución, los coeficientes de las ecuaciones y los términos fuente pierde parcialmente su significado si el método no ha desarrollado medios para tener en cuenta las representaciones polinómicas por partes, en particular , el aparato para la integración exacta de polinomios sobre elementos de la malla dual, subdominios de elementos y segmentos de bordes de borde. Como consecuencia, los resultados de los cálculos utilizando los esquemas construidos deben considerarse desde el punto de vista de los efectos de la integración numérica, teniendo en cuenta varios métodos de su implementación; se vuelve mucho más difícil comparar los resultados de la investigación con los trabajos de otros autores, etc. Por lo tanto, este trabajo está dedicado a la revisión de tecnologías MCM/FEM existentes para la construcción de análogos discretos de problemas de tipo convección-difusión. La tecnología para tener en cuenta la representación polinómica por partes de la solución, los coeficientes de la ecuación y los incluidos en las condiciones de contorno, así como los términos fuente en métodos de volúmenes finitos que utilizan espacios de elementos finitos debe cumplir los siguientes requisitos: 1) permitir combinaciones arbitrarias de representaciones polinómicas de coeficientes y soluciones en elementos de partición, así como aumentar el grado de interpolación de polinomios de la representación de la solución local; 2) utilizar principios unificados de aproximación al calcular las contribuciones de elementos correspondientes a varios términos de la ecuación (difusión, convectiva, términos de reacción, términos fuente), así como contribuciones de aristas que aproximan partes de límites con diferentes tipos de condiciones de contorno especificadas en ellos; 3) permitir una generalización homogénea al caso tridimensional; 4) tener en cuenta la experiencia de tecnologías de elementos finitos bien desarrolladas, en particular, el uso de la expansión de bases de espacios de elementos finitos y las ventajas de integrar con precisión representaciones polinómicas por partes de la solución y coeficientes de transferencia; 5) proporcionar una base tecnológica unificada para aproximaciones FEM/O mixtas que utilizan dos conjuntos de funciones de prueba (volumen finito y elemento finito) para aproximar una ecuación; 6) los principios de la tecnología deben permanecer sin cambios durante la transición del uso de espacios de elementos finitos consistentes (métodos de volumen finito/elementos finitos con cálculo de incógnitas en los nodos) al uso de elementos finitos inconsistentes (métodos con cálculo de incógnitas en los centros de aristas de triangulación); 7) la tecnología se puede utilizar para aproximar varias clases de problemas físicos. De las tecnologías existentes de métodos de volumen finito que utilizan espacios de elementos finitos (métodos de volumen/elementos finitos (FVE), métodos de volumen finito/elementos finitos (CVFEM), métodos de subvolumen, métodos de volumen/elementos mixtos (MEV)), ninguna no cumple los requisitos anteriores. Por lo tanto, la creación de nuevas tecnologías para estas clases de métodos que utilizan particiones simpliciales y conjuntos baricéntricos como duales parece ser un tema de investigación relevante. En el caso de un predominio significativo de la convección, la comparación de varios esquemas de discretización de MCO, así como la comparación de los cálculos utilizando el método de elementos finitos y el método de volúmenes finitos, en realidad se reduce a una comparación de los esquemas correspondientes en contra del viento. Los más estudiados y utilizados con frecuencia en el caso no estructurado son los esquemas contra el viento de la clase de métodos de volumen finito con el cálculo de variables en los centros de las celdas. A pesar de que los bordes de los elementos de partición no son paralelos a los ejes de coordenadas, estos esquemas en la mayoría de los casos son de naturaleza unidimensional, ya que se reducen a resolver el problema de la descomposición de una discontinuidad en las líneas que conectan los centroides de símplex. Los cálculos que utilizan tales esquemas no reproducen la estructura multidimensional del flujo y tienen una difusión numérica excesiva. Para construir esquemas de aproximación de segundo orden ascendentes es necesaria una expansión significativa de la plantilla, lo que en el caso no estructurado conduce a una complicación significativa de las estructuras de datos correspondientes. Los esquemas anteriores para los esquemas con el cálculo de incógnitas en los nodos de triangulación y los puntos medios de sus bordes son actualmente pocos (ver). En algunos casos, el principio de aproximación ascendente se reduce a utilizar un valor de una sustancia escalar (en un nodo simplex que se encuentra aguas arriba, o dos valores ponderados) en los extremos de un borde simplex que se encuentra aguas arriba. Sólo uno de los esquemas conocidos, el FLO (Flow Oriented Upwind Scheme), desarrollado por K. Prakash y S. Patankar, aprovecha el cálculo de incógnitas en los nodos: la capacidad de construir funciones de perfil asimétricas. Pero los cálculos que utilizan este esquema se consideran insatisfactorios, ya que el esquema no tiene la propiedad de ser positivo y los procesos iterativos a menudo divergen. Estimar la difusión numérica introducida por el uso de esquemas contra el viento en cuadrículas simples es un problema en sí mismo. Los trabajos existentes en esta dirección, que proporcionan estimaciones teóricas de las características de convergencia, se limitan a una variedad de esquemas para calcular variables en los centros de celdas. Por lo tanto, es de particular importancia estimar la tasa de convergencia de los esquemas MCO/FE a barlovento utilizando una serie de experimentos numéricos. Por lo tanto, la construcción y el análisis comparativo de esquemas MCO/FE a barlovento en redes no estructuradas es un tema de investigación actual. El objetivo del trabajo es desarrollar tecnologías computacionales para métodos de volúmenes finitos utilizando espacios de elementos finitos para aproximar problemas de tipo convectivo-difusión. Para lograr este objetivo, se formularon los siguientes objetivos de investigación: 1) mejora de tecnologías para discretizar sistemas de leyes de conservación utilizando el método de volumen finito/elementos finitos sobre mallas simpliciales, utilizando particiones baricéntricas como particiones duales; 2) desarrollo de tecnologías para la aproximación de problemas de tipo convectivo-difusión con primeras derivadas significativas; construcción, implementación y análisis comparativo de esquemas upstream en redes no estructuradas, en particular, realización de experimentos computacionales para evaluar el orden de aproximación de los esquemas propuestos y conocidos más precisos, así como comparación de las características de los esquemas upstream basados en MCE/FE y MEF; 3) creación, a partir de las tecnologías desarrolladas, de paquetes de software que permitan simular adecuadamente flujos viscosos e incompresibles de líquidos y gases en áreas geométricamente complejas, en casos estacionarios y no estacionarios. Métodos de búsqueda. Métodos de matemáticas computacionales. Análisis comparativo de tecnologías para la integración exacta de polinomios en métodos de elementos finitos, volúmenes/elementos finitos, residuos distribuidos. Evaluación experimental de la tasa de convergencia de esquemas de flujo a barlovento para problemas con solución analítica. Cálculos sobre un conjunto de particiones condensadas de elementos finitos, seguidos de análisis de convergencia a datos experimentales. La novedad científica del trabajo es la siguiente: 1. Se propone una nueva tecnología para tener en cuenta la representación polinómica por partes de la solución, los coeficientes de transferencia y los términos fuente al discretizar problemas con valores de frontera inicial utilizando los métodos de volúmenes/elementos finitos, volúmenes/elementos finitos y subvolúmenes. La tecnología se basa en el uso de la expansión básica de espacios de elementos finitos en términos de coordenadas baricéntricas simpliciales, con una mayor integración exacta de sus monomios. Para los esquemas MKO/FE, MKO/E con cálculo de variables en nodos de triangulación, se proponen tres clases de fórmulas para la integración exacta de monomios de coordenadas baricéntricas: sobre segmentos de la malla dual en un elemento, sobre subregiones y segmentos baricéntricos de bordes limítrofes. Para los métodos de subvolumen que utilizan espacios de elementos finitos inconsistentes, se propone utilizar el principio de integración exacta de funciones básicas y se obtienen las fórmulas integrales correspondientes. 2. Se propone un método para construir esquemas MCO/FE a barlovento en cuadrículas simples, basado en la aproximación separada de flujos de masa y valores de sustancias escalares en segmentos de la cuadrícula dual. Se introducen los conceptos de matriz local de coeficientes de peso de un esquema contracorriente, interna a los elementos de los esquemas, y positividad local de los esquemas. Se ha propuesto un esquema de contraflujo de clase exponencial y se ha construido su análogo para el MKO con el cálculo de símplex desconocidos en baricentros. 3. Se obtuvieron estimaciones experimentales de la tasa de convergencia del esquema de ceñida con ponderación de flujos másicos y el esquema de clases exponencial propuesto. Utilizando soluciones del tipo capa límite, se analizó la estabilidad de los esquemas construidos y se comparó con los esquemas FEM aguas arriba. 4. Utilizando las tecnologías de aproximación propuestas para problemas de tipo convección-difusión, se creó un conjunto de programas para modelar flujos viscosos incompresibles en variables naturales de velocidad-presión y se llevaron a cabo una serie de experimentos computacionales que confirmaron la efectividad de los esquemas construidos. Estructura y alcance de la tesis. La disertación consta de una introducción, cuatro capítulos, una conclusión, una lista de referencias, un apéndice y contiene 173 páginas, incluidas 10 tablas y 51 figuras. La bibliografía contiene 117 títulos.
Disertaciones similares en la especialidad "Modelado matemático, métodos numéricos y paquetes de software", 13.05.18 código HAC
Método numérico para calcular flujos de gas viscoso compresible en una amplia gama de números de Mach 2004, Candidato de Ciencias Físicas y Matemáticas Chirkov, Denis Vladimirovich
Método para el estudio numérico del flujo alrededor de configuraciones espaciales mediante la resolución de las ecuaciones de Navier-Stokes basadas en esquemas de precisión de alto orden. 2010, Doctor en Ciencias Físicas y Matemáticas Volkov, Andrey Viktorovich
Modelado numérico del movimiento de un fluido viscoso incompresible con límites libres utilizando el método de vecinos naturales generalizado. 2008, Candidata de Ciencias Físicas y Matemáticas Rein, Tatyana Sergeevna
Desarrollo de tecnología informática de alta precisión basada en el método espectral de elementos finitos 2007, candidato de ciencias físicas y matemáticas Poponin, Vladimir Sergeevich
Estudio de flujos de fluidos viscosos en canales de forma compleja. 2002, candidato de ciencias físicas y matemáticas Firsov, Dmitry Konstantinovich
Conclusión de la tesis. sobre el tema "Modelado matemático, métodos numéricos y paquetes de software", Voitovich, Tatyana Viktorovna
Conclusión
Este trabajo está dedicado al desarrollo de tecnologías computacionales para métodos de volúmenes finitos en mallas simpliciales, utilizando espacios de elementos finitos y particiones baricéntricas como duales para aproximar problemas de tipo convectivo-difusión. El trabajo obtuvo los siguientes resultados principales para la defensa:
1. Se propone una nueva tecnología para tener en cuenta la representación polinómica por partes de la solución, los coeficientes de transferencia y los términos fuente al discretizar problemas con valores de frontera inicial utilizando los métodos de volúmenes/elementos finitos, volúmenes/elementos finitos y subvolúmenes. La tecnología se basa en el uso de la expansión básica de espacios de elementos finitos en términos de coordenadas baricéntricas simpliciales, con una mayor integración exacta de sus monomios. Para los esquemas MKO/FE, MKO/E con cálculo de variables en nodos de triangulación, se proponen tres clases de fórmulas para la integración exacta de monomios de coordenadas baricéntricas: sobre segmentos de la malla dual en un elemento, sobre subregiones y segmentos baricéntricos de bordes limítrofes. Para los métodos de subvolumen que utilizan espacios de elementos finitos inconsistentes, se propone utilizar el principio de integración exacta de funciones básicas y se obtienen las fórmulas integrales correspondientes.
2. Se propone un método para construir esquemas MCO/FE a barlovento en cuadrículas simples, basado en la aproximación separada de flujos de masa y valores de sustancias escalares en segmentos de la cuadrícula dual. Se introducen los conceptos de matriz local de coeficientes de peso de un esquema ascendente, interna a los elementos de los esquemas, y positividad local de los esquemas. Se ha propuesto un esquema de contraflujo de clase exponencial y se ha construido su análogo para el MKO con el cálculo de símplex desconocidos en baricentros.
3. Se obtuvieron estimaciones experimentales de la tasa de convergencia del esquema de contraflujo con ponderación de flujos másicos y el esquema de clases exponencial propuesto. Utilizando soluciones del tipo capa límite, se analizó la estabilidad de los esquemas construidos y se comparó con los esquemas FEM aguas arriba. Se muestra que los esquemas MCO/FE completos permiten rastrear las características de las soluciones de la capa límite con mucha más precisión que los esquemas del método de Petrov-Galerkin con funciones de base asimétricas (polinomios de Legendre), los esquemas de elementos finitos de Rice y Schnipke, así como esquemas combinados de elementos finitos de orden superior de aproximación desarrollados por T. Sheu, S. Wang y S. Tsai.
4. Utilizando los esquemas de aproximación propuestos para problemas de tipo convección-difusión, se creó un conjunto de programas para modelar flujos viscosos incompresibles en variables naturales velocidad-presión, en mallas combinadas, utilizando polinomios de interpolación de presión y velocidad del mismo orden; Se llevaron a cabo una serie de experimentos computacionales para confirmar la efectividad de los circuitos construidos.
5. Para un flujo de referencia en un canal detrás de un paso hacia atrás, se muestra por primera vez la interacción del efecto de entrada y el efecto de usar aproximaciones aguas arriba.
Por lo tanto, la tecnología propuesta en el trabajo para discretizar problemas de valores de frontera inicial utilizando el método de elemento finito/volumen finito en cuadrículas simpliciales es una forma efectiva de aproximar sistemas de leyes de conservación; los esquemas desarrollados contra el viento tienen buenas características de convergencia y el uso de Los métodos de discretización para un sistema de ecuaciones de Navier-Stokes con el mismo orden de interpolación para los componentes del vector velocidad-presión permiten obtener resultados que concuerdan bien con los datos experimentales. Las clases de métodos de volumen finito/elementos finitos sobre mallas simpliciales, cuya base tecnológica es la integración exacta de monomios de coordenadas baricéntricas, son métodos eficaces para modelar flujos viscosos incompresibles en áreas con geometría de límites compleja.
Lista de referencias para la investigación de tesis. Candidata de Ciencias Físicas y Matemáticas Voitovich, Tatyana Viktorovna, 2000
1. Belotserkovsky O.M., Modelado numérico en mecánica continua. M.: Ciencia. Cabeza. ed. fisica y matematicas literatura, 1984.
2. A. S. Boldarev, V. A. Gasilov. O. G. Olkhovskaya, Hacia la solución de ecuaciones hiperbólicas en cuadrículas no estructuradas // Modelado matemático. 1996. T.8, núm. 3. págs. 51-78.
3. P. A. Voinovich, D. M. Sharov, Modelado de flujos de gas discontinuos en redes no estructuradas // Modelado matemático. 1993. T. 5. Núm. 7, págs. 86-114.
4. I. J1. Guryeva, Tecnología computacional del método de volúmenes finitos // Dis. para el título de Candidato en Ciencias. f.-m. Ciencia. Novosibirsk 1997. - 115 p.
5. Zhukov M.F., Solonenko O.P., Chorros de polvo de alta temperatura en el procesamiento de materiales en polvo. Novosibirsk ES SB RAS. 1990.
6. V. P. Ilyin, Esquemas de diferencias equilibradas de mayor precisión en cuadrículas rectangulares no uniformes. Novosibirsk 1994. - 31 páginas (Preimpresión/CC SB RAS No. 1031).
7. Ilyin V.P., Turakulov A.A., Sobre aproximaciones de equilibrio integro de problemas de valores límite tridimensionales. Novosibirsk, 1993. - 24 p. - (Preimpresión/CC SB RAS: No. 986).
8. V. M. Kovenya, N. N. Yanenko, Método de división en problemas de dinámica de gases. Novosibirsk, Ciencia. 1989.
9. A. Ladyzhenskaya, Problemas matemáticos en la dinámica de fluidos viscosos e incompresibles. M.: Tqc. editorial f.-m. iluminado.- 1961.
10. D. Oden, Elementos finitos en mecánica continua no lineal. M.: Mir, 1976.
11. Patankar S., Métodos numéricos para resolver problemas de transferencia de calor y dinámica de fluidos. -METRO.:. Energoatomizdat, 1984.
12. N. Pissanetski S. Tecnología de matrices dispersas. M.: Mir. 1988.
13. Preparata F. Sheimos M. Geometría computacional; Introducción. M."Mir, 1984.
14. A. A. Samarsky, Introducción a la teoría de los esquemas de diferencias. M.: Nauka, 1971.
15. L Segerlind, Aplicación del método de los elementos finitos M.: Mir. 1979
16. N. K. Sukanek, R. P. Rhodes, Formulación de la condición sobre el eje de simetría en el cálculo numérico de flujos simétricos // Rocketry and Cosmonautics, 1978. Vol. 16. No. 10). págs. 96-98.
17. R. Temam, Ecuaciones de Navier-Stokes, Teoría y análisis numérico // M.: Mir. 1981.
18. K. Fletcher, Métodos numéricos basados en el método Galerkin II M.: Mir, 1991
19. D. Shi, Métodos numéricos en problemas de transferencia de calor. METRO.; Mundo, 1988.
20. G. Schlichting, Teoría de la capa límite. M.: Editorial extranjera. iluminado. 1956.
21. E. P. Shurina, T. V. Voitovich, Análisis de algoritmos para métodos de elementos finitos y volúmenes finitos en mallas no estructuradas al resolver las ecuaciones de Navier-Stokes // Tecnologías computacionales. 1997. T. 2. No. 4. P. 84104.
22. E. P. Shurina, O. P. Solonenko, T. V. Voitovich, Nueva tecnología del método de volúmenes finitos en rejillas simpliciales para problemas de tipo convectivo-difusión. Novosibirsk 1999. -51 e.- (Preimpresión/ ITAM SB RAS; No. 8-99).
23. I. Yu. Chumakov, “Uso de diferentes condiciones de presión en el límite de salida al calcular flujos internos complejos de fluidos incompresibles en rejillas combinadas”, Vestn. ellos dicen científicos. Ser. Matemáticas aplicadas y mecánica. 1997. T 1. P. 55-62.
24. N. N. Yanenko, Método de pasos fraccionarios para resolver problemas multidimensionales de física matemática. Novosibirsk: Nauka, 1967.
25. Un manual de elementos finitos. Agencia Nacional de Métodos y Estándares de Elementos Finitos //NEL. Glasgow, 1986.
26. K. Ajmani, WF Ng. EM. Lion, Métodos de gradiente conjugado precondicionado para las ecuaciones de Navier-Stokes//J. Computadora. Física. 1994. vol. 1 10. págs. 68-81.
27. F. Angrand, A Dervieux, Algunos esquemas triangulares explícitos de elementos finitos para las ecuaciones de Euler // Int. J.paraNúmero. Métodos en Fluidos. 1984. vol. 4. págs. 749-764.
28. P. Arminjon, A. Dervieux, Construcción de viscosidades artificiales TVD-Hke en rejillas FEM arbitrarias bidimensionales // J. Comput. Phys., 1993. Vol. 106. págs. 176-198.
29. B. Armaly, F. Durst, J. C. F. Pereira, B. Schoenung, Investigación experimental y teórica del flujo escalonado hacia atrás //J. Mecánica de fluidos. 1983. vol. 127.473496.
30. F. Babuska, Límites de error para métodos de elementos finitos//Numer. Matemáticas. 1971 Vol.16. Págs. 322-333.
31. Babuska, B. A. Szabo, I. N. Katz, La versión p del método de elementos finitos // SIAM J. Numer. Anal. 1981. vol. 18. págs. 516-544.
32. P. Balland, E. Suli, Análisis del método de volumen finito de vértice de celda para problemas hiperbólicos con coeficientes variables // SIAM J. Numer. Anal. 1997. vol. 34. págs. 1127-1151.
33. R. E. Bank, B. D. Welfert, Estimaciones de error a posteriori para el problema de Stokes // SIAM J. Numer. Anal. 1991. vol. 28. págs. 591-623.
34. T. J. Barth, D. C. Jespersen, El diseño y aplicación de esquemas contra el viento en mallas no estructuradas // Documento AIAA 89-0336.
35. E. Barton, Un estudio numérico del flujo sobre un escalón confinado hacia atrás // Int. J.ForNumer. Métodos en Fluidos. 1995. vol. 21. págs. 653-665.
36. E. Barton, El efecto de entrada del flujo laminar sobre una geometría escalonada orientada hacia atrás // Int. J.paraNúmero. Métodos en Fluidos. 1995. vol. 25. págs. 633-644.
37. S. Benharbit, A. Chalabi, J. P Vila, Viscosidad numérica y convergencia de métodos de volumen finito para leyes de conservación con condiciones de contorno // SIAM J. Nu-mer. Anal. 1995. vol. 32. P 775-796.
38. Z. Cai, Sobre el método del elemento de volumen finito //Numer. Matemáticas. 1991 vol. 58 pág. 713735.
39. Z. Cai, S. McCormick, Sobre la precisión del método de elementos de volumen finito para ecuaciones de difusión en rejillas compuestas // SIAM J. Numer. Anal. 1990. vol. 27. págs. 636-655.
40. Z. Cai, J. Mandel, S. McCormick, El método del elemento de volumen finito para ecuaciones de difusión en triangulaciones generales // SIAM J. Numer. Anal. 1991 Vol. 28. P. 392402.
41. M. C. Ciccoli, Algoritmos de descomposición de dominio adaptativo y aproximación de volumen finito/elementos finitos para ecuaciones de advección-difusión // Journal of Scientific Computing. 1996. Vol. 11. P 299-341.
42. P. Chatzipantelidis, Un método de volumen finito basado en el elemento Crouzeix-Raviart para PDE elípticas en dos dimensiones //Numer. Math. 1999, Vol. 82. P. 409-432.
43. K. H. Chen, R H. Pletcher, Variable primitiva: procedimiento de cálculo fuertemente implícito para flujos viscosos a todas las velocidades // AIAA J. 1991. Vol. 29. P1241-1249.
44. S. Chou, D. Kwak, P. S. Vassilevski, Métodos de covolumen mixto para problemas elípticos en cuadrículas triangulares // SIAM J. Numer. Anal. 1998. vol. 35. pág. 1850-1861.
45. Christie, D. F. Griffiths, A. R. Mitchell y O. C. Zienkiewicz, Métodos de elementos finitos para ecuaciones diferenciales de segundo orden con primeras derivadas significativas // Int. J. Número. Métodos Ing. 1976. vol. 10. 1389-1396.
46. J.-P. Croisille, esquemas de cajas de volumen finito // Proc. de Segundo Interno. Síntoma. sobre volúmenes finitos para aplicaciones complejas, 19-22 de julio de 1999, Duisburg, Alemania. Publicaciones científicas HERMES, París, 1999.
47. V. Cockburn, F. Coquel. P. G. Lefloch, Convergencia del método del volumen finito para leyes de conservación multidimensionales // SIAM J. Numer. Anal. 1995. vol. 32.687-705.
48. L. Davidson, Un método de corrección de presión para mallas no estructuradas con volúmenes de control arbitrarios // Int. J. de Número. Métodos en Fluidos. 1998. vol. 22. págs. 265-281.
49. C. Debiez, A. Dervieux, K. Meg, B. Nkonga, Cálculo de flujos inestables con métodos mixtos de volumen finito/elementos finitos contra el viento // Int. J. de Número. Métodos en Fluidos. 1998. vol. 27. págs. 193-206.
50. M. Delanaye, J. A. Essers, Esquema de volumen finito de reconstrucción cuadrática para flujos compresibles en redes adaptativas no estructuradas // AIAA Journal. 1997. vol. 35. págs. 631-639.
51. Dervieux A., Simulación Steady Euler utilizando mallas no estructuradas // Serie de conferencias VKI. 1985. N° 1884-04.
52. Eisenberg M. A., Malvern L. E., Sobre la integración de elementos finitos en coordenadas naturales // Int. J. Número. Métodos Ing. 1973. vol. 7. 574-575.
53. A. Fezoui, Clase de esquemas implícitos contra el viento para simulaciones de Euler con mallas no estructuradas // J. Sotr. Física. 1989. vol. 84. págs. 174-206.
54. C. Gallo, G. Manzini, Un enfoque mixto de elementos finitos/volumen finito para resolver el transporte de biodegradación en aguas subterráneas // Int. J. de Número. Métodos en Fluidos.1998. vol. 26. págs. 533-556.
55. T. Gallouet, J. P. Vila, Esquemas de volumen finito para leyes de conservación de tipo mixto // SIAM J. Numer. Anal. 1991. vol. 28. págs. 1548-1573.
56. P. M. Gresho, S. T. Chan, R. L. Lee, G. D. Upson, Un método de elementos finitos modificado para resolver lo dependiente del tiempo. Ecuaciones incompresibles de Navier-Stokes. Parte 2: Aplicaciones // Int. J. de Número. Métodos en fluidos, 1984. Vol. 4. pág. 619640.
57. A. Grundmann, H. M. Moller, Fórmulas de integración invariantes para i-simplex mediante métodos combinacionales // SIAM J. Numer. Anal 1978 vol. 15, págs. 282-290.
58. W. Hackbusch, Sobre esquemas de cajas de primer y segundo orden // Computación. 1989. vol. 41. págs. 277-296.
59. L. P. Hackman, G. D. Raithby, A. B. Strong. Predicciones numéricas de flujos sobre pasos hacia atrás // Int. J. de Número. Métodos en Fluidos. 1984. vol. 4. Pág. 71 1-724.
60. L. Hallo, C. Ribault, M. Buffat, Un método implícito mixto de volumen finito y elementos finitos para resolver flujos compresibles turbulentos en 3D. J. de métodos numéricos en fluidos, 1997. vol. 25. págs. 1241-1261.
61. F. H. Harlow, J. E. Welch, Cálculo numérico del flujo de fluido incompresible con viscosidad dependiente del tiempo con superficie libre // Phys. Fluidos. 1965. vol. 8. pág. 21822189.
62. F. Ilinca, D. Pelletier, A. Garon, Un método adaptativo de elementos finitos para un modelo de turbulencia de dos ecuaciones en flujos delimitados por paredes. J. de Número. Métodos en Fluidos. 1997. vol. 124. Págs. 101-120.
63. E. Issman, G. Degrez, H. Deconinck, Distribución residual implícita a contraviento de Euler y Navier-Stokes Solver sobre mallas no estructuradas // AIAA Journal, 1996. Vol. 1, núm. 34. pág. 2021-2028.
64. J. P. Jessee, W. A. Fiveland, “Un algoritmo de vértice de celda para las ecuaciones incompresibles de Navier-Stokes en cuadrículas no ortogonales”, Int. J. de Número. Métodos en Fluidos. 1996. vol. 23. págs. 271-293.
65. Jianguo H., Shitong X., Sobre el método de elementos de volumen finito para problemas elípticos autoadjuntos generales // SIAM .J Numer. Anal. 1998. vol. 35. pág. 1762-1774.
66. M. Lallemand, H. Steve, A. Dervieux, Multigridding no estructurado por aglomeración de volumen: estado actual // Computers Fluids, 1992 vol. 21. págs. 397-433.
67. Y. Liu, M. Vinokur, Integración exacta de polinomios y fórmulas de cuadratura simétrica sobre cuadrículas poliédricas arbitrarias // J. Comput. Física. 1998. vol. 140. págs. 122-147.
68. D. Marcum, Modelos de turbulencia para cálculos de elementos finitos no estructurados // Int. J.ForNumer. Métodos en Fluidos. 1995, vol. 20. págs. 803-817.
69. C. Masson, H. I. Saabas, B. R. Baliga, Método de elementos finitos de volumen de control de igual orden coubicado para flujo de fluido incompresible axialmente bidimensional // Int J. For Numer. Métodos en Fluidos. 1994. vol. 18. págs. 1-26.
70. S. Mattiussi, Un análisis de finito vol. Métodos de elementos finitos y diferencias finitas utilizando algunos conceptos de topología algebraica // J. Comput. Física. 1997. vol. 133. págs. 289-309.
71. D. Mavriplis, Solución multicuadrícula de ecuaciones bidimensionales de Euler en mallas triangulares no estructuradas // AIAA Journal, 1988. Vol 26. P. 824-831.
72. P. R. McHugh, D. A. Knoll, “Soluciones de volumen finito totalmente acopladas de Navier-Stpkes incompresibles y ecuaciones de energía utilizando un método de Newton inexacto”, Int. J. Para Número. Métodos en Fluidos. 1994. vol. 19. págs. 439-455.
73. Y. Murthy, S. Mathur, Flujo periódico y transferencia de calor mediante mallas no estructuradas // Int. J. de Número. Métodos en Fluidos. 1997. vol. 25. págs. 659-677.
74. S. Muzaferija, D. Gosman, Procedimiento CFD de volumen finito y estrategia de control de errores adaptativo de cuadrículas de topología arbitraria // J. Comput. Phys., 1997, vol. 138. págs. 766-787
75. P. Nithiarasu, O. C. Zienkiewlcz, V. V. K. Satya Sai, K. Morgan, R. Codina, M. Vazquez, Viscosidades de captura de impacto para el algoritmo general de mecánica de fluidos // Int. J. de Número. Métodos en Fluidos. 1998. vol. 28. págs. 1325-1353.
76. K. Ohmori, T. Ushijima, Una técnica de tipo ascendente aplicada a una aproximación lineal no conforme de elementos finitos de ecuaciones de difusión convectiva // R.A.I.R.O. Anal. Número.
77. D. Pan, J. C. Cheng, Cálculos de Navier-Stokes de volumen finito a barlovento sobre mallas triangulares no estructuradas // AIAA Journal, 1993. Vol. 1, núm. 31. págs. 1618-1625.
78. S. V. Potapov, Un algoritmo mixto FE FV en dinámica de sólidos no lineal // Proc. de Segundo Interno. Síntoma. sobre volúmenes finitos para aplicaciones complejas. 19-22 de julio de 1999. Duisburg, Alemania. - Publicaciones científicas HERMES. París. 1999. pág. 271278.
79. C. Prakash, S. V. Patankar, Un método de elementos finitos basado en volumen de control para resolver las ecuaciones de Navier-Stokes utilizando interpolación velocidad-presión de igual orden //Numer. Transferencia de calor. 1985. vol. 8. págs. 259-280.
80. S. Ramadhyani, S. V. Patankar, Solución de la ecuación de Poisson: comparación de los métodos de Galerkin y de volumen de control // Int. J. Número. Métodos Ing. 1980. vol. 15.1395-1418.
81. Rida S., McKenty F., Meng F. L., Reggio M., Un esquema de control de volumen escalonado para rejillas triangulares no estructuradas // Int. J. de Número. Métodos en Fluidos. 1995. vol. 25. págs. 697-717.
82. P. L. Roe, solucionadores de Riemann aproximados, vectores de parámetros y esquemas de diferencia //! Sotr. Física. 1981. vol. 43. págs. 357-372.
83. C. Rohde, Esquemas de volumen finito a favor del viento para sistemas hiperbólicos débilmente acoplados de leyes de conservación en 2D // Numer. Matemáticas. 1998. vol. 81. págs. 85-123.
84. Tony W. H. Sheu, S. K. Wang, S. F. Tsai, Desarrollo de un esquema de alta resolución para una ecuación multidimensional de advección-difusión // J. Sotr. Física. 1998. vol. 144. pág. 1-16.
85. Saad Y., Métodos iterativos para sistemas lineales dispersos. PSW Publishing Co., Boston, MA, 1995.
86. V. V. K. S. Sai, O. C. Zienkiewicz, M. T. Manzari, P. R. M. Lyra, K. Morgan, Propósito general versus algoritmos especiales para flujos de alta velocidad con choques // Int. J. Número. Metanfetamina. Fluidos. 1998. vol. 27. págs. 57-80.
87. J. L. Sohn, Evaluación de FIDAP en algunos puntos de referencia laminares y turbulentos clásicos // Int. J. de Número. Métodos en Fluidos. 1988. vol. 8. págs. 1469-1490.
88. En Stoufflet, Investigación de la división generalizada de vectores de flujo para flujos compresibles en mallas triangulares // Int. J. de Número. Métodos en Fluidos. 1995. vol. 20. págs. 1047-1059.
89. B. Stouflette. J. Periaux, F. Fezoui, A. Dervieux, Simulación numérica de flujos hipersónicos de Euler en 3-D alrededor de vehículos espaciales utilizando elementos finitos adaptados // AIAA Paper 87-0560.
90. C. Taylor, P. Hood, Una solución numérica de las ecuaciones de Navier-Stokes utilizando la técnica de elementos finitos // Computadoras y fluidos. 1973. vol. 1. pág. 73-100.
91. Thomadakis M, Leschziner M., Un método de corrección de presión para la solución de flujos viscosos incompresibles en rejillas no estructuradas // Int.J. para métodos numéricos en fluidos. -1996. vol. 22 P 581-601.
92. A. K. Verma, V. Eswaran, Enfoque de control de volumen superpuesto para problemas de convección-difusión // Int. J. de Número. Métodos en Fluidos. 1996. vol. 23. págs. 865-882.
93. M. M. T. Wang, T. W. H. Sheu, Sobre un elemento finito compacto de orden mixto para resolver las ecuaciones tridimensionales incompresibles de Navier-Stokes // Int. J. de Número. Métodos en Fluidos. 1997. vol. 25. págs. 513-522.
94. M. M. T. Wang, T. W. H. Sheu, Implementación de una condición de frontera libre para las ecuaciones de Navier-Stokes // Int. J. Número. Métodos Calor y flujo de fluidos, 1997. Vol.7. Pág. 95-111.
95. D. Winterscheidt, K. S. Surana, formulación de elementos finitos de mínimos cuadrados versión p para flujo de fluido bidimensional e incompresible // Int. J. Número. Metanfetamina. Fluidos, 1994. Vol. 18. págs. 43-69.
96. A. M. Winslow, Solución numérica de la ecuación cuasilineal de Poisson en una malla triangular no uniforme, J. Comput. Física. 1967. vol. 2. 149-172.
97. A. Younes, R. Mose. P. Ackerer. G. Chavent, una nueva formulación del método mixto de elementos finitos para resolver PDE elípticas y parabólicas con elementos triangulares // J. Comput. Phys., 1999. vol. 149. págs. 148-167.
98. P.J. Zwart, G. D. Raithby, M. J. Raw, El método integrado de volumen finito espacio-tiempo y su aplicación a problemas de límites en movimiento // J. Comput. Física. 1999. vol. 154. págs. 497-519.
99. O. C. Zienkiewicz, El método de los elementos finitos en la ciencia de la ingeniería // McGraw-Hill London. 1971.
100. OC Zienkiewicz, R. Codina, Un algoritmo general para flujo compresible e incompresible. Parte 1: El esquema dividido basado en características // Int. J. Número. Metanfetamina. Fluidos. 1995. vol. 20. págs. 869-885.
101. S. M. Rhie y W. L. Chow, Un estudio numérico del flujo turbulento que pasa por un perfil aerodinámico aislado con separación del borde de salida // AIAA Paper No. 82-0998. mil novecientos ochenta y dos.
102. R. I. Issa, Solución de las ecuaciones de flujo de fluidos implícitamente discretizadas mediante división por operadores // J. Computadora. Física. vol. 62. pág. 40-65.1985.
103. J. Kim, S. J. Kline, J. P. Johnston, Investigación de una capa de corte turbulenta que se vuelve a unir: flujo sobre un escalón orientado hacia atrás, Journal of Fluids Eng., vol. 102, págs. 302-308.117. http//www.ict.nsc.ru/linpar
Tenga en cuenta que los textos científicos presentados anteriormente se publican únicamente con fines informativos y se obtuvieron mediante el reconocimiento de texto de tesis original (OCR). Por tanto, pueden contener errores asociados a algoritmos de reconocimiento imperfectos. No existen tales errores en los archivos PDF de disertaciones y resúmenes que entregamos.
Hace algún tiempo estaba buscando una descripción de las operaciones y procesos que ocurren en la biblioteca de modelado numérico OpenFOAM. Encontré muchas descripciones abstractas del funcionamiento del método de volúmenes finitos, esquemas de diferencias clásicos y varias ecuaciones físicas. Quería saber con más detalle: ¿de dónde provienen estos valores en tal o cual archivo de salida en tal o cual iteración, qué expresiones hay detrás de ciertos parámetros en los archivos de configuración fvSchemes, fvSolution?
Para aquellos que también estén interesados en esto, este artículo. Aquellos que conocen bien OpenFOAM o los métodos implementados en él, escriben sobre los errores e inexactitudes encontradas en un mensaje personal.
Ya había un par de artículos sobre OpenFOAM en Habré:
Por lo tanto, no me detendré en el hecho de que es “una plataforma abierta (GPL) para simulación numérica, diseñada para simulaciones asociadas con la resolución de ecuaciones diferenciales parciales utilizando el método de volúmenes finitos, y es ampliamente utilizada para resolver problemas en mecánica continua”.
Hoy usaré un ejemplo simple para describir las operaciones que ocurren durante los cálculos en OpenFOAM.
Entonces, dada la geometría, un cubo con un lado de 1 metro:
Nos enfrentamos a la tarea de modelar la propagación del flujo de un determinado campo escalar (temperatura, cantidad de materia), que viene dada por la siguiente ecuación de transporte (1) dentro del volumen del cuerpo.
(1) ![]() ,
,
Donde una cantidad escalar, por ejemplo, expresa la temperatura [K] o la concentración de una determinada sustancia, y expresa la transferencia de una sustancia, el flujo másico [kg/s].
Esta ecuación se utiliza, por ejemplo, para modelar la propagación del calor. ![]() ,
,
donde k es la conductividad térmica y es la temperatura [K].
El operador de divergencia es en realidad
operador.
Permítanme recordarles que existe un operador nabla (operador Hamilton), que se escribe de la siguiente manera: ![]() ,
,
Donde i, j, k son vectores unitarios.
Si multiplicamos escalarmente el operador nabla por una cantidad vectorial, obtenemos la divergencia de este vector:
"Desde el punto de vista de la física, la divergencia de un campo vectorial es un indicador de hasta qué punto un punto dado en el espacio es una fuente o un sumidero de este campo"
Si multiplicas el operador nabla por un escalar, obtienes el gradiente de ese escalar:
Un gradiente muestra un aumento o disminución en alguna dirección en la magnitud de un escalar.
Las condiciones de contorno del problema son las siguientes: hay una cara de entrada, una cara de salida y las caras restantes son paredes lisas.

Dividir el volumen de un cubo en volúmenes finitos
Nuestra cuadrícula será muy simple: dividimos el cubo en 5 celdas iguales a lo largo del eje Z.
Muchas fórmulas
El método del volumen finito establece que (1) en forma integral (2) se cumplirá para cada volumen finito.
(2)![]() ,
,
¿Dónde está el centro geométrico del volumen final?
Centro del volumen final

Simplifiquemos y transformemos el primer término de la expresión (2) de la siguiente manera:
(2.1) (HJ-3.12)*
Como puede ver, asumimos que la cantidad escalar cambia linealmente dentro del volumen finito y el valor de la cantidad en algún punto dentro del volumen finito se puede calcular como:
Para simplificar el segundo término de la expresión (2), utilizamos el teorema generalizado de Gauss-Ostrogradsky: la integral de la divergencia del campo vectorial sobre el volumen es igual al flujo vectorial a través de la superficie que limita el volumen dado. En lenguaje humano, “la suma de todos los flujos hacia/desde un volumen finito es igual a la suma de los flujos a través de las caras de este volumen finito”:
(2.3)![]() ,
,
¿Dónde está la superficie cerrada que limita el volumen?
- vector dirigido a lo largo de la normal al volumen.
Vector S

Considerando que el volumen finito está limitado por un conjunto de caras planas, la expresión (2.3) se puede transformar a la suma de integrales sobre la superficie:
(2.4) (HJ-3.13)
,
Donde expresa el valor de la variable en el centro de la cara,
- vector de área, que sale del centro de la cara, se aleja de la celda (localmente), de la celda con un índice más bajo a la celda con un índice más alto (global).
Un poco más sobre el vector S
Para no almacenar los mismos parámetros vectoriales dos veces, porque Es obvio que para dos celdas vecinas, el vector normal al borde entre las celdas, alejado del centro de la celda, diferirá solo en el signo de dirección. Por lo tanto, se creó una relación propietario-vecino entre el borde y la celda. Si el vector de área (dirección global positiva desde una celda con un índice más bajo a una celda con un índice más grande) indica DESDE el centro de la celda, tal relación entre la celda y el vector, y más precisamente entre la celda y el cara, se indica propietario). Si este vector apunta dentro de la celda en cuestión, entonces el vecino. La dirección afecta el signo del valor (+ para el propietario y - para el vecino) y esto es importante al sumar, ver más abajo.
Acerca de los esquemas de diferencia
El valor en el centro de la cara se calcula a través de los valores en los centros de las celdas adyacentes; este método de expresión se denomina esquema de diferencias. En OpenFOAM, el tipo de esquema de diferencia se especifica en el archivo /system/fvSchemes:DivSchemes (predeterminado ninguno; div(phi,psi) Gauss lineal;)
Gauss- significa que se selecciona el esquema de diferencia central;
lineal- significa que la interpolación desde los centros de las celdas a los centros de las caras se producirá de forma lineal.

Supongamos que nuestra cantidad escalar cambia linealmente dentro del volumen finito desde el centro hasta los bordes. Luego se calculará el valor aproximado en el centro de la cara según la fórmula:
¿Dónde están los pesos y se calculan como
¿Dónde están los volúmenes de las células?
Para los casos de celdas sesgadas, existen fórmulas más complejas para calcular los pesos de aproximación.
Por lo tanto, los valores de phi_f en los centros de los bordes de las celdas se calculan en función de los valores en los centros de las celdas. Los valores de gradiente grad(phi) se calculan en función de los valores de phi_f.
Y todo este algoritmo se puede representar en forma del siguiente pseudocódigo.
1. Declaramos un array de gradientes de volúmenes finitos, lo inicializamos con ceros 2. Recorremos todas las caras internas (que no son límite) > Calculamos flux_f = phi_f*S_f. Calcule los valores de phi_f en función de los valores de phi en centavos de celda > Agregue flux_f al gradiente del elemento propietario y -flux_f al gradiente del elemento vecino 3. Itere sobre todas las caras límite > Calcule flux_f = phi_f*S_f > Agregue flux_f al gradiente del elemento propietario (vecino: las caras límite no tienen elementos) 4. Repasemos todos los elementos > Divida la suma del gradiente resultante por el volumen del elemento
muestreo de tiempo

Teniendo en cuenta (2.1) y (2.4), la expresión (2) toma la forma:
(3)
Según el método del volumen finito se realiza una discretización del tiempo y la expresión (3) se escribe como:
(4)
Integramos (4):
(4.1)![]()
Dividamos los lados izquierdo y derecho en:
(5)
Datos para la matriz de muestreo.
Ahora podemos obtener un sistema de ecuaciones lineales para cada volumen finito.A continuación se muestra la numeración de los nodos de la cuadrícula que usaremos. 
Las coordenadas de los nodos se almacenan en /constant/polyMesh/points
24
((0 0 0)
(1 0 0)
(0 1 0)
(1 1 0)
(0 0 0.2)
(1 0 0.2)
(0 1 0.2)
(1 1 0.2)
(0 0 0.4)
(1 0 0.4)
(0 1 0.4)
(1 1 0.4)
(0 0 0.6)
(1 0 0.6)
(0 1 0.6)
(1 1 0.6)
(0 0 0.8)
(1 0 0.8)
(0 1 0.8)
(1 1 0.8)
(0 0 1)
(1 0 1)
(0 1 1)
(1 1 1))
Numeración de nodos-centros de celdas (50, 51 - centros de caras límite): 
Numeración de nodos del centro de la cara: 
Volúmenes de elementos:
Coeficientes de interpolación necesarios para calcular valores en las caras de las celdas. El subíndice "e" indica el "borde derecho de la celda". A la derecha de la vista, como en la figura “Numeración de nodos-centros de celdas”:
Formación de la matriz de muestreo.
Para P = 0.
Expresión (5) que describe el comportamiento de la cantidad.

Se transformará en un sistema de ecuaciones algebraicas lineales, cada una de la forma:
O, según los índices de puntos en las caras.
Y todos los flujos hacia/desde una celda se pueden expresar como una suma.

Donde, por ejemplo, es el coeficiente de linealización del flujo en el punto central de la celda E,
- coeficiente de linealización del flujo en el punto central de la cara,
- parte no lineal (por ejemplo, constante).
Según la numeración de las caras, la expresión tomará la forma: 
Teniendo en cuenta las condiciones de contorno para el elemento P_0, la ecuación algebraica lineal se puede representar como
...sustituir los coeficientes obtenidos previamente...

El flujo de la entrada "a se dirige al interior de la celda y, por tanto, tiene un signo negativo.
Dado que en nuestra expresión de control también tenemos, además del término de difusión, un término de tiempo, pero la ecuación final se ve así
Para P = 1.
Para P = 4.
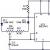
Un sistema de ecuaciones algebraicas lineales (SLAE) se puede representar en forma matricial como
A(i,j) === 40,5 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40,5
psi = dimensiones; Lista no uniforme de campo interno
A partir de lo cual se obtienen los valores del vector.
Luego, el vector se sustituye en el SLAE y se produce una nueva iteración del cálculo del vector.
Y así sucesivamente hasta que la discrepancia alcance los límites requeridos.