Tinklų konstravimas baigtinio tūrio metodui. Ribinio tūrio metodas. Kubo tūrio padalijimas į baigtinius tūrius
Šio metodo pranašumas yra tas, kad jis pagrįstas gamtosaugos įstatymais. Todėl, priešingai nei baigtinių skirtumų metodas, valdymo tūrio metodas užtikrina konservatyvią skaitinę schemą, leidžiančią gauti sprendimus, kurių tikslumas yra priimtinas net ir santykinai grubiuose tinkleliuose.
Pagrindinė metodo idėja yra gana paprasta ir lengvai pritaikoma fiziniam aiškinimui. Diskretuojant Reinoldso vidurkio Navier-Stokes lygtis, skaičiavimo sritis yra padalinta į daugybę nesutampančių elementarių tūrių, todėl kiekviename tūryje yra tik vienas skaičiavimo (mazginis) taškas. Elementariųjų tūrių rinkinys vadinamas skaičiavimo tinkleliu. Tinklelio ląstelės gali būti įvairių formų. Dažniausiai naudojami šešiaedrai (heksaedrai) ir tetraedrai (tetraedrai). Valdymo tūrio metodas leidžia naudoti ląsteles su savavališku skaičiumi veidų (piramidės, prizmės, sudėtingos daugiasluoksnės ir kt.).
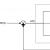
(1)–(18) lygčių sistemos sprendimas pavaizduotas kaip norimų parametrų reikšmių rinkinys šių tūrių centruose. Pavyzdžiui, jei padalinsime kambario tūrį į 1000 atskirų elementarių tūrių (ląstelių), tada tirpalo rezultatas bus 1000 temperatūros, greičio, slėgio ir tt reikšmių. 2 paveiksle parodytas skaičiavimo srities fragmentas. Ląstelės sunumeruotos indeksais i, j, k.
Ryžiai. 2. Skaičiavimo srities fragmentas
Diferencialinių lygčių integravimas atliekamas kiekviename elementiniame tūryje. Integralai apskaičiuojami naudojant interpoliacijos formules, kurios naudojamos norint nustatyti norimų kintamųjų reikšmes tarp skaičiuojamų taškų. Dėl to gaunamas diskretinis pradinių lygčių analogas mazginiuose taškuose, kuris atspindi tiriamų kintamųjų išliekamumo dėsnį kiekviename baigtiniame tūryje.
Pažymėtina, kad daugumoje šiuolaikinių skaičiavimo hidrodinaminių paketų, tokių kaip „STAR-CD“, „FLUENT“, „CFX“ ir daugelyje kitų, modelio lygtims diskretizuoti yra įdiegtas valdymo tūrio metodas.
Skaičiavimo tinkleliai
Tinklo konstravimo procesas yra vienas iš pagrindinių skaitmeninio eksperimento atlikimo momentų. Nagrinėjamai problemai tinkamo skaičiavimo tinklelio parinkimas ir sukūrimas yra gana sudėtinga ir daug laiko reikalaujanti procedūra. Racionalus tinklelio pasirinkimas gali žymiai supaprastinti skaitinį problemos sprendimą.

Ryžiai. 3. Tinklelio ląstelių konfigūracijos
Tinklelio langeliai gali būti įvairių formų (3 pav.) ir dydžių, kurie geriausiai tinka konkrečiai problemai spręsti. Paprasčiausias tinklelio tipas yra tada, kai ląstelės yra identiškos ir turi kubinę formą.
Paprastai šalia kietų paviršių tinklelis tampa tankesnis, ty ląstelės yra mažesnio dydžio, normaliai paviršiui. Tai daroma siekiant pagerinti skaičiavimų tikslumą tose srityse, kuriose tiriamų parametrų srauto gradientai kinta greičiau, pavyzdžiui, ribiniame sluoksnyje.
Galite padidinti skaičiavimų tikslumą ir sumažinti apytikslę paklaidą dviem būdais:
· atrankos tikslumo eiliškumo didinimas;
· tinklelio žingsnio mažinimas.
Sprendžiant nestacionarias problemas, ląstelių dydžiai Δx ir laiko integravimo žingsnis Δt yra susiję su CFL (Courant-Friedrichs-Levy) sąlyga:  , u- greitis.
, u- greitis.
Šiuo metu inžinerinėje praktikoje naudojamos universalios kompiuterinės programos leidžia dirbti su savavališkais nestruktūriniais tinkleliais naudojant labai iškreiptus elementus. Šiuo atveju diskretizacijos tikslumo tvarka, kaip taisyklė, neviršija sekundės. Norint gauti kokybišką sprendimą, būtina sukonstruoti skaičiavimo tinklelius mažais žingsneliais.
STAR-CCM paketas perėjo prie daugiakampių ląstelių (panašių į futbolo kamuolį), kurios, sujungus ląsteles, pašalina labai iškreiptas ląsteles.
Pagrindinis nestruktūruotų akių privalumas, palyginti su įprastomis, yra didesnis lankstumas diskretuojant sudėtingos formos fizinę sritį. Šiuo atveju tinklelio langeliai turi turėti palyginamus tūrius arba plotus ir neturi susikirsti. Tačiau šio tipo tinklelio trūkumai yra tinklelio matmenų padidėjimas. Kaip rodo praktika, tam pačiam objektui teisingai sukonstruotas nestruktūrizuotas tinklelis turi maždaug dvigubai daugiau langelių nei struktūrizuotas, o tai natūraliai padidina skaičiavimo laiką, palyginti su įprastais tinklais. Tačiau daugeliu atvejų nestruktūruoti tinkleliai yra vienintelis galimas konstrukcijos variantas dėl objekto geometrijos sudėtingumo. Be to, racionaliai pasirinkus tinklelio algoritmą, laikas, praleistas nestruktūrizuoto tinklelio konstravimui, yra žymiai mažesnis nei laikas, reikalingas struktūriniam (blokinės struktūros) tinkleliui sukurti. Dėl to bendras laikas, sugaištas sprendžiant problemą (įskaitant susirišimo laiką ir skaičiavimo laiką), gali būti daug mažesnis, kai naudojami nestruktūrizuoti tinkleliai, nei struktūrinių tinklelių atveju.
Reikiamo tinklelio dydžio nustatymas yra labai sudėtinga užduotis. Universalus metodas, kuriuo reikėtų vadovautis renkantis tinklelio matmenis, yra susijęs su tuo, kad gautas sprendimas neturėtų keistis, kai didėja langelių skaičius (tinklelio konvergencija).
Esant tipinėms problemoms, tinklelio konvergencijos tyrimo atlikti nebūtina, nes galite pasikliauti anksčiau gautais rezultatais. Pereinant tirti naujo tipo problemą, būtina atlikti tinklelio konvergencijos tyrimą ir nustatyti skaičiavimo tinklelio reikalavimus.
Atkreipkite dėmesį, kad sprendžiant realias vėdinimo ir oro kondicionavimo problemas, būdingas elementų skaičius, kaip taisyklė, yra nuo 500 tūkst. iki 3 - 4 mln., priklausomai nuo objekto geometrinio sudėtingumo, reikalingų parametrų rinkinio ir jo specifikos. problema. Tokiu atveju klasteryje, kurį sudaro, pavyzdžiui, iš 24 branduolių, skaičiavimo laikas gali siekti iki savaitės, o sprendžiant nestacionarias problemas – iki kelių savaičių.
STAR-CCM+ pakete yra modulis, skirtas skaičiavimo tinkleliams kurti. Taip pat yra atskiri tinklelių generavimo paketai, pavyzdžiui, plačiai naudojamas ANSYS, ICEM CFD (ICEM). Išoriniuose paketuose įmontuotus tinklelius galima importuoti į STAR-CCM+ paketą.
1 skyrius. Apsaugos dėsnių sistemų diskretizavimo metodai.
1.1. Pradinių-ribinių reikšmių uždavinių diskretizacijos metodų technologiniai principai naudojant baigtinių elementų erdves.
1.1.1. Baigtinių elementų metodai.
1.1.2. Ribinio tūrio metodai.
1.2. Priešvėjinės schemos ant paprastų tinklelių.
1.3. Stacionarios Navier-Stokes lygčių sistemos sprendimo metodai.
2 skyrius. Konvekcinės-difuzijos-reakcijos lygčių diskrečiųjų analogų konstravimas baigtinio tūrio metodu
2.1. Konvekcinės difuzijos tipo problemų MKO/FE diskretizavimas.
2.1.1. Trianguliacija ir dvigubo tinklelio konstravimo metodas.
2.1.2. Integrali gamtosaugos įstatymų forma.
2.1.3. Difuzijos srautų aproksimacija ir MKO/FE standumo matricos apskaičiavimas.
2.1.4. Šaltinio terminų aproksiminimas.
2.1.5. MCO/FE masės matricos apskaičiavimas.
2.1.6. Kraštinių sąlygų apskaita.
2.2. Daugiamačių priešvėjinių schemų konstravimas ant paprastų tinklelių.
2.2.1. Konvekcinių lokalinių matricų skaičiavimas.
2.2.2. Schemos su svėrimo masės srautais.
2.2.3. Eksponentinių schemų modifikavimas.
2.2.4. Kai kurios priešsrovių schemų savybės ir jų konstravimo principai.
2.2.5. Eksponentinės schemos analogas schemoms su nežinomųjų skaičiavimu ląstelių centruose.
2.3. Naujos MKO integralų formulių klasės.
2.3.1. Baricentrinių koordinačių monomijų integravimas.
2.3.2. Apie galimus daugianario vaizdų derinius.
2.3.3. Dėl lokalinio sprendinio vaizdavimo interpoliacijos polinomų eilės didinimo.
2.4.4. Nenuoseklių baigtinių elementų naudojimas.
2.4. Elementarus globalių matricų surinkimas
3 skyrius. Klampių nesuspaudžiamų terpių srauto lauko modeliavimas.
3.1. Matematinis modelis.
3.2. Integrali gamtosaugos įstatymų forma.
3.3. Atsižvelgiant į greičio ir slėgio laukų ryšį.
3.3.1. Ry-Chow interpoliacija masės srautams apskaičiuoti.
3.3.2. Tęstinumo lygties diskretizavimas.
3.3.3. Ribų su nuliniu masės srautu apskaita.
3.3.4. Bendroji iteracijos schema 1.
3.4. Iteratyvių schemų konvergencijos spartinimas.
3.4.1. Slėgio ir greičio laukų korekcija
3.4.2. Bendroji iteracijos schema II.
3.5. Tiesinių algebrinių lygčių sistemų sprendimas.
4 skyrius. Skaitiniai eksperimentai.
4.1. Ribinio sluoksnio tipo sprendimų stabilumo analizė.
4.2. Greitėjantis srautas apvaliame vamzdyje.
4.3. Srautas pradinėje sklandaus kanalo dalyje.
4.4. Laminarinis purkštuko srautas iš taškinio antgalio (šaltinio purkštukas)
4.5. Laminarinis srautas už plokščio asimetrinio nugaros laiptelio
4.5.1. Skaičiavimas naudojant įvairias priešsrovių schemas
4.5.2. Įvesties efektas skaičiuojant srautus už žingsnio atgal naudojant MKO/FE paprastuose tinkleliuose.
4.5.3. Skirtingų tiesinių algebrinių lygčių sistemų sprendimo metodų palyginimas.
Rekomenduojamas disertacijų sąrašas
Klampaus nesuspaudžiamo skysčio vidinių srautų modeliavimas baigtinių elementų metodu naudojant priešpriešinio srauto schemas 2007 m., fizinių ir matematikos mokslų kandidatas Gobysh, Albina Vladimirovna
Skaitinės schemos, pagrįstos baigtinio tūrio / baigtinių elementų aproksimacija, skirtos išspręsti ilgųjų bangų hidrodinamikos uždavinius 2004 m., fizinių ir matematikos mokslų kandidatas Styvrinas, Andrejus Vadimovičius
Lygiagrečios technologijos ribinių verčių uždaviniams spręsti 2005 m., fizinių ir matematikos mokslų daktaras Vasilevskis, Jurijus Viktorovičius
Baigtinio tūrio metodas konvekcijos-difuzijos problemoms ir dviejų fazių srauto modeliams 2010 m., fizinių ir matematikos mokslų kandidatas Nikitinas, Kirilas Dmitrijevičius
Trimatis priemaišų perdavimo procesų modeliavimas sudėtingos struktūros poringose terpėse 2007 m., fizinių ir matematikos mokslų kandidatas Kapyrinas, Ivanas Viktorovičius
Disertacijos įvadas (santraukos dalis) tema „Baigtinio tūrio/baigtinių elementų metodo technologijos paprastuose tinkleliuose konvekcinio difuzinio tipo problemoms spręsti“
Matematinės fizikos uždavinių skaitinis sprendimas yra vienas pagrindinių realių reiškinių tyrimo metodų. Kombinuotas skaičiavimo ir fizikinių eksperimentų naudojimas analizuojant bet kokį reiškinį leidžia, viena vertus, sumažinti brangių eksperimentinių matavimų skaičių, kita vertus, patikrinti ir tobulinti matematinius modelius.
Didėjant skaičiavimo sistemų spartai, skaitiniams matematinės fizikos uždavinių sprendimo metodams keliami nauji reikalavimai. Svarbi tyrimų sritis yra šiuolaikinių gamtosaugos dėsnių diskretavimo metodų, suteikiančių galimybę imituoti vis naujas problemų klases ir gauti žymiai geresnių rezultatų sprendžiant žinomas, kūrimas ir tobulinimas.
Šiuolaikiniai skaičiavimo algoritmai turėtų pateikti tiksliausią sudėtingos geometrijos sričių aprašymą. Tai įmanoma naudojant nestačiakampius ir nestruktūrinius tinklelius. Palyginti su savavališkais nestačiakampiais tinkleliais, nestruktūrizuotų paprastų tinklelių atveju (dviejų dimensijų atveju trianguliacija ir trimačiu atveju padalijimas į tetraedrus), vietinį kondensaciją lengviau įgyvendinti (pavyzdžiui, už nugaros laiptelio, zonoje). staigus susiaurėjimas, šalia tvirtinimo taško), taip pat, jei reikia, skaičiavimo tinklelio pritaikymas priklausomai nuo sprendimo elgsenos. Taigi, net ir diskretuojant išsaugojimo dėsnius geometriškai paprastose srityse, kurias galima tiksliai pavaizduoti stačiakampių elementų rinkiniu, nestruktūruoti paprasti tinkleliai turi daug privalumų. Nepaisant akivaizdžių nestruktūrizuotų tinklelių pranašumų, skirtų aproksimuoti savavališkus regionus ir galimybės automatiškai sudaryti paprastas pertvaras, jie praktiškai nebuvo naudojami skaičiavimo skysčių dinamikoje ir tik per pastaruosius 15 metų tapo vis populiaresni. Remiantis B. Stoufflett ir kt. parodymais, to priežastis yra smarkiai ilgėjantis skaičiavimo laikas pereinant prie nestruktūrizuotų metodų. Faktas yra tas, kad nulinių elementų padėtis diskrečiųjų analogų matricose priklauso nuo tinklelio mazgų gretimumo ir savavališkai, matricos saugomos naudojant universalius formatus ir duomenų struktūras. Retos matricos dauginimo iš vektoriaus ir nepilnos faktorizavimo operacijos tampa daug „brangesnės“. Tuo pačiu metu skaičiavimo skysčių dinamikos lygčių sistemos yra tarpusavyje susijusios netiesinės lygčių sistemos, kurių implicitinio sprendimo schemos turi daugiapakopį iteracinį pobūdį, todėl kiekvienoje „pasaulinėje“ iteracijoje reikia išspręsti kelias tiesinės algebrinės lygtys. Atsiradus galingoms skaičiavimo sistemoms, taip pat sukūrus adaptyviuosius ir daugiatinklinius metodus, atsirado galimybė naudoti nestruktūrizuotus tinklelius ir atitinkamas erdvinės diskretizacijos schemas hidro-dujų dinaminiams procesams modeliuoti.
Dažniausias diskretizavimo metodas nestruktūrizuotu atveju yra baigtinių elementų metodas (FEM). Atkreipkime dėmesį į tokius metodo privalumus, kaip diferencialinių operatorių savarankiškos dalies simetriškumo išsaugojimas jų diskrečiuose analoguose (tai pasiekiama specialiai parinkus testavimo funkcijų erdvę, sutampančią su bandomųjų funkcijų erdve) , galimybė padidinti aproksimacijos tikslumą didinant lokalinio sprendinio vaizdavimo interpoliacijos polinomų laipsnį (vadinamosios FEM p ir h-p versijos, ), natūralus antrojo ir trečiojo tipo kraštinių sąlygų svarstymas. Visų pirma baigtinių elementų metodas turi nusistovėjusį technologinį pagrindą
Vidinių sandaugų aproksimavimo metodai, darant prielaidą, kad ribinės reikšmės uždavinio sprendimas ir parametrai yra nuosekliai daugianariai, būtent: atitinkamos baigtinių elementų erdvės bazinio skaidymo naudojimas, integralinių formulių klasės, kurios leidžia tiksliai integruoti savavališką. pagrindinių funkcijų per pertvaros elementus ir elementų briaunas (paviršius) produktai,
Standartinis interpoliacijos aparatas.
Metodo technologijos leidžia paprastai ir vienodai sukurti diskrečius pradinių ribinių reikšmių uždavinių analogus su įvairaus tipo ribinėmis sąlygomis, darant prielaidą, kad sprendimas yra lygus ir lygčių koeficientų polinominis elgesys yra padalintas. ribinės sąlygos, .
Daugelyje programų, pvz., modeliuojant viršgarsinius ir transoninius dujų srautus ir atliekant skaičiavimus naudojant sekliojo vandens modelius, labai svarbus yra vietinis konservatyvumas schemose, naudojamose išsaugojimo dėsniams diskretizuoti. Baigtinių elementų metodas neleidžia pakankamai tiksliai atsekti atsirandančių nenuoseklių sprendimų ypatybių, o tradicinis tokių problemų sprendimo būdas yra baigtinio tūrio metodas. Diskretuojant tvermės dėsnių sistemą baigtinio tūrio metodu, skaičiavimo sritis aproksimuojama atvirų baigtinių tūrių aibe, tada tyrėjas žengia „žingsnį atgal“, pereidamas prie pradinės lygčių sistemos integralios formos; Naudodami Ostrogradskio-Gausso formulę, pereiname nuo tūrio integravimo prie ribinio integralo, todėl srautų per baigtinių tūrių paviršius aproksimavimo metodas visiškai nustato skaičiavimo schemą. Pasak S. Patankaro monografijos, "daugumai mokslininkų, dirbančių hidrodinamikos ir šilumos perdavimo srityje, baigtinių elementų metodas vis dar atrodo apgaubtas paslapties. Variacinė formuluotė ir net Galerkino metodas nėra tinkamas paprastam fiziniam aiškinimui". Tuo pačiu metu baigtinio tūrio schemos turi tam tikrą fizinę srautų ir šaltinio terminų balanso reikšmę kiekviename baigtiniame tūryje, kuris apytiksliai atitinka skaičiavimo sritį, todėl baigtinio tūrio metodas tampa patrauklesnis. MKO „paprastumas“ yra viena iš priežasčių, kodėl metodui trūksta bendros technologinės bazės.
Taigi, klasikinės MKO versijos (ribinio tūrio / baigtinio skirtumo metodas, FVDM) pranašumai apima vietinį diskrečių schemų konservatyvumą, didesnį paprastumą ir aiškumą bei galimybę natūraliai atsižvelgti į antrojo tipo ribines sąlygas. Be to, sprendžiant problemas, kai vyrauja konvekcija, supaprastinamas priešpriešinio srauto schemų įgyvendinimas, nes srautai per baigtinių tūrių paviršius yra ir analizuojami, ir apytiksliai dydžiai.
Bandymai susisteminti baigtinių tūrių aproksimacijas lėmė dalinį FEM technologijų ir integracijos per baigtinius tūrius principo derinį; ankstyviausi iš jų siekia B. R. Baliga, K. Prakash ir S. Patankar darbus ir yra žinomi kaip CVFEM metodai (kontroliniu tūriu pagrįsti baigtinių elementų metodai), toliau vadinami baigtinių tūrio / baigtinių elementų metodais (FVM/). FE). Metodo autoriai siekė sukonstruoti konservatyvias baigtinio tūrio metodo schemas, panaudojant vieną iš pagrindinių FEM privalumų – galimybę aproksimuoti sudėtingas geometrijas naudojant nestruktūrinius tinklus. Profilio funkcijos šioje metodų klasėje yra „pagalbinio pobūdžio“, sprendinio priklausymas baigtinių elementų erdvėms neakcentuojamas. Baricentriniai rinkiniai naudojami kaip dvigubas skaidinys.
Pirmą kartą baigtinio tūrio/baigtinio skirtumo metodo (MKO/KR, FVDM) universalių technologinių principų nebuvimo problema aptariama Z. Kaya darbe „Apie baigtinį tūrio/elemento metodą“. Autorius atkreipia skaitytojo dėmesį į „ribinio tūrio/ribinio skirtumo metodo nesistemiškumą“; Aproksimuojant tvermės dėsnių sistemas baigtinio tūrio/baigtinio skirtumo metodu, tame pačiame darbe gali būti naudojami skirtingų klasių aproksimacijos, o tai labai apsunkina tokių schemų konvergencijos analizę. Siūlomas šios problemos sprendimas – baigtinių elementų metodo (sprendinio ieškojimas kokioje nors baigtinių elementų erdvėje ir srautams skaičiuojant panaudojant sprendinio fragmentinį polinominį elgesį) ir integralios tvermės dėsnių formos bendras panaudojimas. Taigi baigtinio tūrio/elementų metodai (FME/E, „box method“, FVE) atsirado bandant sukurti „sistemingesnes baigtinio tūrio technologijas“. Bendrųjų technologinių principų nebuvimas baigtinio tūrio/ribinio skirtumo metoduose taip pat pažymimas Ya. JI darbuose. Guryeva ir V.P. Iljinas.
Baigtinio tūrio / baigtinių elementų metodai (FVE) ir baigtinių tūrių / baigtinių elementų metodai (CVFEM) naudoja nuoseklias funkcijų baigtinių elementų erdves, tiesias simpleksams ir priklauso ląstelių ir viršūnių baigtinių tūrių schemų klasei, pav. 1, a.
Daugelyje skaičiavimo skysčių dinamikos schemų (klampių nesuspaudžiamų srautų modeliavimas) naudojamos nenuoseklios baigtinių elementų erdvės, ypač Crousey-Raviard erdvė, kuri yra tiesinė ant elementų, ištisinių bandymo funkcijų kraštų centruose. S. Choi ir D. Kwak pasiūlė baigtinio tūrio metodus, naudojant nenuoseklias baigtinių elementų erdves, juos ištyrė daugybė kitų autorių darbų (vadinamieji subtūrio metodai, covolume metodas) ir yra schemos su nežinomųjų skaičiavimo centruose. kraštų ( Dažniausios dujų dinamikos problemų sprendimo ir antropogeninių nelaimių modeliavimo schemos naudojant sekliųjų vandenų lygtis yra į ląstelę orientuotos baigtinio tūrio schemos, pav. 1, f Jų populiarumą lemia tai, kad skaičiuojant nežinomuosius centroiduose, daugumą dujų dinamikos schemų (S.K. Godunovo schemų, TVD schemų) galima perkelti į nestruktūrizuotus tinklus be esminių technologinių pakeitimų. o a in 1 pav. Skaičiavimo taškų vieta FE tinklo mazgų atžvilgiu. Šiame darbe visų pirma nagrinėjamos baigtinio tūrio metodų klasės su nežinomųjų skaičiavimu trianguliacijos mazguose (MKO/E, MKO/FE) ir briaunų centruose (subtūrio metodai), ateityje taip pat sakysime „baigtinio tūrio metodai naudojant baigtinių elementų erdves. “ Remiantis daugybe tyrimų (, ), šios metodų klasės, skirtos konvekcinės difuzijos problemoms spręsti, suteikia geresnes sprendimo apytiksles nei metodai su nežinomųjų ląstelių centruose skaičiavimu. Viena iš pagrindinių priežasčių yra ta, kad naudojant aukščiau išvardintus metodus išsaugomas pirmųjų dvigubo tinklelio elementų testavimo funkcijų išvestinių tęstinumas. Veiksmingas būdas sprendžiant problemas, kai vyrauja konvekcija, yra Galerkin metodo naudojimas su simetrinėmis testavimo funkcijomis diferencialinių operatorių savaime adjunktinei daliai ir prieš srovę MCO schemos jų asimetrinei daliai, vadinamajai. mišriųjų baigtinių elementų/tūrio metodai (FEM/O, MEV, mišriųjų elementų/tūrio metodas). Disertacinis darbas visų pirma skirtas baigtinio tūrio metodo technologijoms tobulinti nurodytoms metodų klasėms (MKO/E, MKO/CE, FEM/O, potūrio metodai). Šiuo metu šie metodai neturi nusistovėjusių technologijų, leidžiančių atsižvelgti į atskirą sprendinio daugianario elgesį, šaltinio terminus ir perdavimo koeficientus. Galime išvardyti šias aparato, skirto tiksliam daugianarių integravimui baigtinių tūrių metoduose, naudojant baigtinių elementų erdves, netobulumo priežastis: 1. Skirtingai nuo baigtinių elementų metodo, baigtinio tūrio metodas neturi p versijos, nes įvedus papildomus mazgus ir kelių tipų dvigubus tinklelius, daugelio išsaugojimo dėsnių sistemos kintamųjų santykio vietinis konservatyvumas. į „svetimus“ baigtinius tūrius yra pažeidžiamas. Taigi aproksimacijos apsiriboja žemesnės eilės baigtinių elementų erdvėmis. 2. Palyginti su baigtinių elementų metodu, baigtinio tūrio metodai pasižymi didesne laisve renkantis testo funkcijų erdves, kurios šiuo atveju, pasirodo, yra susijusios su nežinomųjų skaičiavimo taškų išsidėstymu diskretizavimo atžvilgiu. mazgai (schemos su nežinomųjų išsidėstymu mazguose, briaunų vidurio taškais, centroidų simpleksais) ir dvigubo tinklelio konstravimo metodas (naudojant baricentrines, ortocentrines, cirkumcentrines aibes). Kartu su galimybe naudoti vienoje vietoje esančius arba išdėstytus tinklelius, tai suteikia visą esamų MCM schemų įvairovę kiekvienoje programoje. Taikant MCM metodus, skirtus konservavimo dėsniams, kuriuose naudojamos baigtinių elementų erdvės, diskretizuoti, kruopštus šių erdvių pasirinkimas sprendimams, lygčių koeficientai ir šaltinio terminai iš dalies praranda prasmę, jei metodas neturi sukurtų priemonių, leidžiančių atsižvelgti į padalytas daugianario reprezentacijas, ypač , aparatas, skirtas tiksliai integruoti polinomus per dvigubo tinklelio elementus, elementų subdomenus ir kraštinių kraštų segmentus. Dėl to skaičiavimų, naudojant sudarytas schemas, rezultatus reikėtų vertinti skaitinės integracijos poveikio požiūriu, atsižvelgiant į įvairius jų įgyvendinimo būdus; darosi žymiai sunkiau lyginti tyrimų rezultatus su kitų autorių darbais ir kt. Taigi, šis darbas skirtas esamų MCM/FEM technologijų, skirtų konvekcinio-difuzijos tipo problemų diskrečiųjų analogų konstravimui, peržiūrai. Technologija, skirta atsižvelgti į sprendinio dalinį daugianario atvaizdavimą, lygties koeficientus ir tuos, kurie yra įtraukti į ribines sąlygas, taip pat šaltinio terminus baigtinio tūrio metoduose, naudojant baigtinių elementų erdves, turi atitikti šiuos reikalavimus: 1) leisti savavališkus koeficientų ir sprendinių daugianarių atvaizdų derinius skaidinių elementuose, taip pat padidinti vietinio sprendinio vaizdavimo interpoliacijos polinomų laipsnį; 2) naudoti unifikuotus aproksimavimo principus apskaičiuojant elementų, atitinkančių įvairius lygties dėmenis (difuzijos, konvekcinės, reakcijos terminus, šaltinio terminus), taip pat indėlius iš briaunų, aproksimuojančių ribų dalis su skirtingomis nurodytomis ribinėmis sąlygomis ant jų; 3) leisti homogeniškai apibendrinti trimačiam atvejui; 4) atsižvelgti į gerai išplėtotų baigtinių elementų technologijų patirtį, ypač į baigtinių elementų erdvių bazių išplėtimo panaudojimą ir tikslaus sprendinio gabalinio daugianario atvaizdų integravimo ir perdavimo koeficientų privalumus; 5) pateikti vieningą technologinį pagrindą mišrioms FEM/O aproksimacijoms, kurios naudoja du testavimo funkcijų rinkinius – baigtinį tūrį ir baigtinį elementą – vienai lygčiai aproksimuoti; 6) technologijos principai turėtų likti nepakitę pereinant nuo nuoseklių baigtinių elementų erdvių naudojimo (baigtinių tūrių/baigtinių elementų metodai su nežinomųjų skaičiavimu mazguose) prie nenuoseklių baigtinių elementų naudojimo (metodai su nežinomųjų skaičiavimo centruose). trikampių briaunų); 7) technologija gali būti naudojama apytiksliai įvertinti įvairias fizinių problemų klases. Iš esamų baigtinių tūrių metodų, naudojančių baigtinių elementų erdves, technologijų (baigtinio tūrio/elemento metodai (FVE), baigtinio tūrio/baigtinių elementų metodai (CVFEM), potūrio metodai, mišrūs tūrio/elemento metodai (MEV)), nė viena neatitinka. aukščiau nurodytus reikalavimus. Taigi naujų technologijų kūrimas šioms metodų klasėms naudojant paprastas pertvaras ir baricentrinius rinkinius kaip dvigubas, atrodo, yra aktuali tyrimo tema. Esant dideliam konvekcijos vyravimui, įvairių MCO diskretizacijos schemų palyginimas, taip pat skaičiavimų, naudojant baigtinių elementų metodą ir baigtinio tūrio metodą, palyginimas iš tikrųjų išeina į atitinkamų priešvėjinių schemų palyginimą. Labiausiai ištirtos ir dažniausiai naudojamos nestruktūrizuotu atveju yra baigtinių tūrių metodų klasės priešvėjinės schemos su kintamųjų skaičiavimu ląstelių centruose. Nepaisant to, kad pertvarų elementų briaunos nėra lygiagrečios koordinačių ašims, šios schemos daugeliu atvejų yra vienmatės, nes jos yra skirtos išspręsti pertrūkio nykimo problemą linijose, jungiančiose simpleksų centroidai. Skaičiavimai naudojant tokias schemas neatkuria daugiamatės srauto struktūros ir turi pernelyg didelę skaitinę difuziją. Norint sukurti antrosios eilės aproksimavimo schemas, būtina žymiai išplėsti šabloną, o tai nestruktūrizuotu atveju sukelia reikšmingą atitinkamų duomenų struktūrų komplikaciją. Prieš srovę schemų, skirtų schemoms su nežinomųjų skaičiavimu trikampio mazguose ir jo briaunų vidurio taškais, šiuo metu yra nedaug (žr.). Kai kuriais atvejais prieš srovę taikomas aproksimacijos principas yra naudojamas naudojant vieną skaliarinės medžiagos vertę - viename mazge, esančiame prieš srovę, arba dvi svertines reikšmes - vienakrypčio krašto, esančio prieš srovę, galuose. Tik viena iš žinomų schemų FLO (Flow Oriented Upwind Scheme), kurią sukūrė K. Prakash ir S. Patankar, pasinaudoja nežinomųjų skaičiavimu mazguose – galimybe konstruoti asimetrines profilio funkcijas. Tačiau skaičiavimai naudojant šią schemą laikomi nepatenkinamais, nes schema neturi pozityvumo, o iteraciniai procesai dažnai skiriasi. Apskaičiuoti skaitmeninę difuziją, atsirandančią naudojant priešvėjines schemas paprastose tinkleliuose, yra savaime problema. Esami šios krypties darbai, pateikiantys teorinius konvergencijos charakteristikų įverčius, apsiriboja įvairiomis schemomis, skirtomis kintamiesiems skaičiuoti ląstelių centruose. Todėl ypač svarbu įvertinti priešvėjinių MCO / FE schemų konvergencijos greitį naudojant skaitinius eksperimentus. Taigi, nestruktūrizuotų tinklų priešvėjinių MCO/FE schemų konstravimas ir lyginamoji analizė yra dabartinė tyrimų tema. Darbo tikslas – sukurti skaičiavimo technologijas baigtinių tūrių metodams, naudojant baigtinių elementų erdves, siekiant aproksimuoti konvekcinio-difuzinio tipo problemas. Šiam tikslui pasiekti buvo suformuluoti šie tyrimo tikslai: 1) tvermės dėsnių sistemų diskretizacijos technologijų tobulinimas baigtinio tūrio/baigtinių elementų metodu ant paprastų tinklelių, naudojant baricentrines pertvaras kaip dvigubas pertvaras; 2) konvekcinio-difuzinio tipo problemų aproksimavimo su reikšmingais pirmaisiais dariniais technologijų kūrimas; nestruktūrizuotų tinklų schemų konstravimas, įgyvendinimas ir lyginamoji analizė, ypač skaičiavimo eksperimentų atlikimas, siekiant įvertinti siūlomų ir tiksliausių žinomų schemų aproksimacijos tvarką, taip pat prieš srovę esančių schemų charakteristikų palyginimas, pagrįstas MCE/FE ir FEM; 3) sukurtų technologijų pagrindu sukurtų programinės įrangos paketų, leidžiančių tinkamai imituoti klampius nesuspaudžiamus skysčių ir dujų srautus geometriškai sudėtingose srityse, stacionariais ir nestacionariais atvejais. Tyrimo metodai. Skaičiavimo matematikos metodai. Technologijų lyginamoji analizė tiksliam polinomų integravimui baigtinių elementų metoduose, baigtinių tūrių/elementų, pasiskirstytų liekanų. Eksperimentinis priešvėjo srauto schemų konvergencijos greičio įvertinimas problemoms su analitiniu sprendimu. Sutrumpintų baigtinių elementų pertvarų aibės skaičiavimai, po to atlikta konvergencijos su eksperimentiniais duomenimis analizė. Darbo mokslinė naujovė yra tokia: 1. Pasiūlyta nauja technologija, skirta atsižvelgti į sprendinio, perdavimo koeficientų ir šaltinio dalių fragmentinį daugianario vaizdavimą, kai diskretizuojami pradinės-ribinės reikšmės uždaviniai, naudojant baigtinių tūrių/elementų, baigtinių tūrių/baigtinių elementų ir potūrių metodus. Technologija pagrįsta baigtinių elementų erdvių bazinio išplėtimo naudojimu pagal baricentrines paprastas koordinates, toliau tiksliai integruojant jų vienatūrius. MKO/FE, MKO/E schemoms su kintamųjų apskaičiavimu trikampio mazguose siūlomos trys formulių klasės, skirtos tiksliam baricentrinių koordinačių monomijų integravimui: per dvigubo tinklelio segmentus elemente, virš baricentrinių subregionų ir segmentų. ribinių kraštų. Subtūriniams metodams, naudojantiems nenuoseklias baigtinių elementų erdves, siūloma naudoti tikslios bazinių funkcijų integravimo principą ir gaunamos atitinkamos integralų formulės. 2. Siūlomas priešvėjo MCO/FE schemų konstravimo ant paprastų tinklelių metodas, pagrįstas atskiru masių srautų ir skaliarinių medžiagų verčių aproksimavimu dvigubo tinklelio segmentuose. Supažindinama su priešsrovinės schemos svorių koeficientų lokalios matricos, vidinio schemų elementų ir schemų lokalinio pozityvumo sąvokomis. Pasiūlyta priešpriešinio srauto eksponentinės klasės schema, o jos analogas sukonstruotas MKO su nežinomų simpleksų skaičiavimu baricentruose. 3. Gauti eksperimentiniai priešvėjo schemos su masių srautų svėrimo konvergencijos greičio įverčiai ir pasiūlyta eksponentinė klasių schema. Naudojant ribinio sluoksnio tipo sprendimus, buvo išanalizuotas sukonstruotų schemų stabilumas ir palygintas su priešsrovinėmis FEM schemomis. 4. Taikant siūlomas konvekcinio-difuzijos tipo uždavinių aproksimavimo technologijas, buvo sukurtas programų rinkinys klampių nesuspaudžiamų srautų natūralaus greičio-slėgio kintamuosiuose modeliavimui bei atlikta nemažai skaičiavimo eksperimentų, patvirtinančių sukonstruotų schemų efektyvumą. Disertacijos struktūra ir apimtis. Disertaciją sudaro įvadas, keturi skyriai, išvados, literatūros sąrašas, priedas, 173 puslapiai, iš jų 10 lentelių ir 51 paveikslas. Bibliografijoje yra 117 pavadinimų.
Panašios disertacijos specialybėje „Matematinis modeliavimas, skaitmeniniai metodai ir programiniai paketai“, 05.13.18 kodas HAC
Skaitinis metodas, skirtas apskaičiuoti suspaudžiamų klampių dujų srautus plačiame Macho skaičių diapazone 2004 m., fizinių ir matematikos mokslų kandidatas Chirkovas, Denisas Vladimirovičius
Srauto aplink erdvines konfigūracijas skaitmeninio tyrimo metodas, sprendžiant Navier-Stokes lygtis, pagrįstas didelio tikslumo schemomis 2010 m., fizinių ir matematikos mokslų daktaras Volkovas, Andrejus Viktorovičius
Klampaus nesuspaudžiamo skysčio su laisvomis ribomis judėjimo skaitinis modeliavimas apibendrintu natūralių kaimynų metodu 2008 m., fizinių ir matematikos mokslų kandidatas Reinas, Tatjana Sergeevna
Didelio tikslumo skaičiavimo technologijos, paremtos spektriniu baigtinių elementų metodu, kūrimas 2007 m., fizinių ir matematikos mokslų kandidatas Poponinas, Vladimiras Sergejevičius
Klampių skysčių srautų sudėtingos formos kanaluose tyrimas 2002 m., fizinių ir matematikos mokslų kandidatas Firsovas, Dmitrijus Konstantinovičius
Disertacijos išvada tema „Matematinis modeliavimas, skaitmeniniai metodai ir programinės įrangos paketai“, Voitovičius, Tatjana Viktorovna
Išvada
Šis darbas skirtas baigtinio tūrio metodų skaičiavimo technologijoms kurti ant paprastų tinklelių, naudojant baigtinių elementų erdves ir baricentrines pertvaras kaip dvigubas konvekcinio difuzinio tipo uždaviniams aproksimuoti! Darbe buvo gauti šie pagrindiniai gynybos rezultatai:
1. Pasiūlyta nauja technologija, skirta atsižvelgti į sprendinio, perdavimo koeficientų ir šaltinio dalių fragmentinį daugianario vaizdavimą, kai diskretizuojami pradinės-ribinės reikšmės uždaviniai, naudojant baigtinių tūrių/elementų, baigtinių tūrių/baigtinių elementų ir potūrių metodus. Technologija pagrįsta baigtinių elementų erdvių bazinio išplėtimo naudojimu pagal baricentrines paprastas koordinates, toliau tiksliai integruojant jų vienatūrius. MKO/FE, MKO/E schemoms su kintamųjų apskaičiavimu trikampio mazguose siūlomos trys formulių klasės, skirtos tiksliam baricentrinių koordinačių monomijų integravimui: per dvigubo tinklelio segmentus elemente, virš baricentrinių subregionų ir segmentų. ribinių kraštų. Subtūriniams metodams, naudojantiems nenuoseklias baigtinių elementų erdves, siūloma naudoti tikslios bazinių funkcijų integravimo principą ir gaunamos atitinkamos integralų formulės.
2. Siūlomas priešvėjo MCO/FE schemų konstravimo ant paprastų tinklelių metodas, pagrįstas atskiru masių srautų ir skaliarinių medžiagų verčių aproksimavimu dvigubo tinklelio segmentuose. Supažindinama su priešsrovinės schemos svorių koeficientų lokalios matricos, schemų elementų vidaus ir schemų lokalinio pozityvumo sąvokomis. Pasiūlyta priešpriešinio srauto eksponentinės klasės schema, o jos analogas sukonstruotas MKO su nežinomų simpleksų skaičiavimu baricentruose.
3. Gauti eksperimentiniai priešvėjo schemos su masių srautų svėrimo konvergencijos greičio įverčiai ir pasiūlyta eksponentinė klasių schema. Naudojant ribinio sluoksnio tipo sprendimus, buvo išanalizuotas sukonstruotų schemų stabilumas ir palygintas su priešsrovinėmis FEM schemomis. Parodyta, kad užbaigtos MCO/FE schemos leidžia daug tiksliau sekti ribinių sluoksnių sprendinių požymius nei Petrovo-Galerkino metodo schemos su asimetrinėmis bazinėmis funkcijomis (Legendre polinomais), Rice ir Schnipke baigtinių elementų schemomis, taip pat aukštesnės eilės aproksimacijos kombinuotos baigtinių elementų schemos, sukurtos T. Sheu, S. Wang ir S. Tsai.
4. Taikant siūlomas konvekcinio-difuzinio tipo uždavinių aproksimavimo schemas, sukurtas programų rinkinys, skirtas modeliuoti klampius nesuspaudžiamus srautus natūralaus greičio-slėgio kintamuosiuose, kombinuotuose tinkleliuose, naudojant tos pačios eilės slėgio ir greičio interpoliacinius polinomus; Buvo atlikta daugybė skaičiavimo eksperimentų, siekiant patvirtinti sukonstruotų grandinių efektyvumą.
5. Atskaitos srautui kanale, esančiame už atgalinio žingsnio, pirmą kartą parodyta įvesties efekto ir prieš srovę apytikslių aproksimacijų poveikio sąveika.
Taigi darbe pasiūlyta pradinės ribinės vertės problemų diskretavimo technologija, naudojant baigtinių elementų/baigtinio tūrio metodą ant paprastų tinklelių, yra veiksmingas būdas aproksimuoti išsaugojimo dėsnių sistemas, sukurtos priešvėjinės schemos pasižymi geromis konvergencijos charakteristikomis ir Navier-Stokes lygčių sistemos diskretizacijos metodai su ta pačia greičio ir slėgio vektoriaus komponentų interpoliacija leidžia gauti rezultatus, kurie gerai sutampa su eksperimentiniais duomenimis. Baigtinių tūrių/baigtinių elementų metodų klasės ant paprastų akių, kurių technologinis pagrindas yra tikslus baricentrinių koordinačių monomijų integravimas, yra veiksmingi metodai modeliuoti klampius nesuspaudžiamus srautus sudėtingos ribos geometrijos srityse.
Disertacinio tyrimo literatūros sąrašas fizinių ir matematikos mokslų kandidatas Voitovičius, Tatjana Viktorovna, 2000 m.
1. Belotserkovsky O.M., Skaitinis modeliavimas kontinuuminėje mechanikoje. M.: Mokslas. Galva. red. fizika ir matematika literatūra, 1984 m.
2. A. S. Boldarevas, V. A. Gasilovas. O. G. Olkhovskaya, Nestruktūruotų tinklelių hiperbolinių lygčių sprendimo link // Matematinis modeliavimas. 1996. T. 8, Nr. 3. 51-78 p.
3. P. A. Voinovich, D. M. Sharov, Nutrūkstamų dujų srautų modeliavimas nestruktūrizuotuose tinkleliuose // Mathematical Modeling. 1993. T. 5. Nr.7, 86-114 p.
4. I. J1. Guryeva, Baigtinio tūrio metodo skaičiavimo technologija // Dis. mokslų kandidato laipsniui gauti. f.-m. Sci. Novosibirskas 1997. - 115 p.
5. Žukovas M.F., Solonenko O.P., Aukštos temperatūros dulkėtos purkštukai apdorojant miltelių medžiagas. Novosibirskas IT SB RAS. 1990 m.
6. V. P. Iljinas, Padidinto tikslumo subalansuotų skirtumų schemos ant nevienodų stačiakampių tinklelių. Novosibirskas 1994. - 31 p. (Preprint/CC SB RAS Nr. 1031).
7. Iljinas V.P., Turakulovas A.A., Apie trimačių ribinių reikšmių uždavinių integro-balanso aproksimacijas. Novosibirskas, 1993. - 24 p. - (Preprint/CC SB RAS: Nr. 986).
8. V. M. Kovenya, N. N. Yanenko, Skaldymo metodas dujų dinamikos problemose. Novosibirskas, mokslas. 1989 m.
9. A. Ladyzhenskaya, Matematiniai klampaus nesuspaudžiamo skysčio dinamikos uždaviniai. M.: Tqc. leidykla f.-m. lit.- 1961 m.
10. D. Odenas, Baigtiniai elementai netiesinėje kontinuumo mechanikoje. M.: Mir, 1976 m.
11. Patankar S., Skaitiniai šilumos perdavimo ir skysčių dinamikos uždavinių sprendimo metodai. -M.:. Energoatomizdat, 1984 m.
12. N. Pissanetskis S. Retų matricų technologija. M.: Mir. 1988 m.
13. Preparata F. Sheimos M. Skaičiavimo geometrija; Įvadas. M." Mir, 1984 m.
14. A. A. Samarsky, Įvadas į skirtumų schemų teoriją. M.: Nauka, 1971 m.
15. L Segerlind, Baigtinių elementų metodo taikymas M.: Mir. 1979 m
16. N. K. Sukanek, R. P. Rhodes, Sąlygos simetrijos ašyje formulavimas simetrinių srautų skaitmeniniame skaičiavime // Rocketry and Cosmonautics, 1978. T. 16. Nr. 10). 96-98 p.
17. R. Temam, Navier-Stokes lygtys, teorija ir skaitmeninė analizė // M.: Mir. 1981 m.
18. K. Fletcher, Skaitiniai metodai remiantis Galerkin metodu II M.: Mir, 1991 m.
19. D. Shi, Skaitiniai metodai šilumos perdavimo uždaviniuose. M.; Pasaulis, 1988 m.
20. G. Schlichting, Ribinio sluoksnio teorija. M.: Užsienio leidykla. liet. 1956 m.
21. E. P. Shurina, T. V. Voitovich, Baigtinių elementų ir baigtinių tūrių metodų algoritmų analizė nestruktūrizuotose tinklelėse sprendžiant Navier-Stokes lygtis // Skaičiavimo technologijos. 1997. T. 2. Nr. 4. P. 84104.
22. E. P. Shurina, O. P. Solonenko, T. V. Voitovičius, Nauja baigtinio tūrio metodo technologija ant paprastų tinklelių konvekcinio-difuzinio tipo problemoms spręsti. Novosibirskas 1999. -51 e.- (Preprint/ ITAM SB RAS; Nr. 8-99).
23. I. Yu. Chumakov, "Slėgio prie išėjimo ribos skirtingų sąlygų naudojimas skaičiuojant sudėtingus vidinius nesuspaudžiamo skysčio srautus ant kombinuotų tinklelių", Vestn. jie sako mokslininkai. Ser. Taikomoji matematika ir mechanika. 1997. T 1. P. 55-62.
24. N. N. Yanenko, Trupmeninių žingsnių metodas sprendžiant daugiamačius matematinės fizikos uždavinius. Novosibirskas: Nauka, 1967 m.
25. Baigtinių elementų gruntas. Nacionalinė baigtinių elementų metodų ir standartų agentūra //NEL. Glazgas, 1986 m.
26. K. Ajmani, W-F Ng. M-S. Lion, Navier-Stokes lygčių išankstinio konjuguoto gradiento metodai//J. Comput. Fizik. 1994. T. 1 10. P. 68-81.
27. F. Angrand, A Dervieux, Kai kurios aiškios trikampių baigtinių elementų schemos Eulerio lygtims//Int. J.forNumer. Metodai skysčiuose. 1984. T. 4. P. 749-764.
28. P. Arminjon, A. Dervieux, Konstravimas TVD-Hke Dirbtinės klampos ant Two-Dimensional Arbitrary FEM Grids // J. Comput. Phys., 1993. T. 106. P. 176-198.
29. B. Armaly, F. Durst, J. C. F. Pereira, B. Schoenung, Eksperimentinis ir teorinis atgalinio žingsnio srauto tyrimas //J. Skysčių mechanizmas. 1983. T. 127.473496.
30. F. Babuska, Klaidų ribos baigtinių elementų metodams//Skaičius. Matematika. 1971 T.16. P. 322-333.
31. Babuska, B. A. Szabo, I. N. Katz, Baigtinių elementų metodo p versija // SIAM J. Skaičius. Anal. 1981. T. 18. P. 516-544.
32. P. Balland, E. Suli, Ląstelės viršūnės baigtinio tūrio metodo analizė hiperbolinėms problemoms su kintamaisiais koeficientais // SIAM J. Numer. Anal. 1997. T. 34. P. 1127-1151.
33. R. E. Bank, B. D. Welfert, Stokso problemos a posteriori klaidų įvertinimai // SIAM J. Numer. Anal. 1991. T. 28. P. 591-623.
34. T. J. Barth, D. C. Jespersen, The design and application of upwind systems on unstructured meshes // AIAA paper 89-0336.
35. E. Barton, Skaitmeninis srauto tyrimas per ribotą atgal nukreiptą žingsnį // Tarpt. J.ForNumer. Metodai skysčiuose. 1995. T. 21. P. 653-665.
36. E. Barton, Laminarinio srauto įėjimo efektas per atgal nukreiptą žingsnių geometriją // Tarpt. J.forNumer. Metodai skysčiuose. 1995. T. 25. P. 633-644.
37. S. Benharbit, A. Chalabi, J. P Vila, Numerical viskosity and convergence of finite volume methods for conservation laws with border conditions // SIAM J. Nu-mer. Anal. 1995. T. 32. P 775-796.
38. Z. Cai, Apie baigtinių tūrinių elementų metodą //Skaičius. Matematika. 1991 t. 58 P. 713735.
39. Z. Cai, S. McCormick, Apie baigtinių tūrinių elementų metodo tikslumą difuzijos lygtims kompozitiniuose tinkleliuose // SIAM J. Numer. Anal. 1990. T. 27. P. 636-655.
40. Z. Cai, J. Mandel, S. McCormick, The Finite volume element method for diffusion equations on general triangulations // SIAM J. Numer. Anal. 1991 T. 28. P. 392402.
41. M. C. Ciccoli, Adaptive Domain Decomposition Algorithms and Finite Volume/Finite Element Approximation for Advection-Diffusion Equations // Žurnalas of Scientific Computing. 1996. T. 11. P 299-341.
42. P. Chatzipantelidis, Baigtinio tūrio metodas, pagrįstas Crouzeix-Raviart elementu elipsiniams PDE dviem matmenims //Numer. Math. 1999, Vol. 82. P. 409-432.
43. K. H. Chen, R H. Pletcher, Primitive variable- stipriai implicit skaičiavimo procedūra klampiems srautams visais greičiais // AIAA J. 1991. Vol. 29. P1241-1249.
44. S. Chou, D. Kwak, P. S. Vassilevski, Mixed Covolume method for elliptic problems on triangular grids // SIAM J. Numer. Anal. 1998. T. 35. P. 1850-1861.
45. Christie, D. F. Griffiths, A. R. Mitchell ir O. C. Zienkiewicz, Baigtinių elementų metodai antros eilės diferencialinėms lygtims su reikšmingomis pirmosiomis išvestinėmis // Int. J. Skaičius. Metodai inž. 1976. T. 10. 1389-1396.
46. J.-P. Croisille, Finite Volume Box Schemes // Proc. antrojo stažuotojo. Symp. apie ribotus tomus sudėtingoms programoms, 1999 m. liepos 19–22 d., Duisburgas, Vokietija. HERMES mokslo leidiniai, Paryžius, 1999 m.
47. V. Cockburn, F. Coquel. P. G. Lefloch, Baigtinio tūrio metodo konvergencija daugiamačiams išsaugojimo dėsniams // SIAM J. Skaičius. Anal. 1995. T. 32.687-705.
48. L. Davidson, Slėgio korekcijos metodas nestruktūrizuotoms akims su savavališkais valdymo tūriais // Int. J. už skaičių. Metodai skysčiuose. 1998. T. 22. P. 265-281.
49. C. Debiez, A. Dervieux, K. Meg, B. Nkonga, Nepastovių srautų skaičiavimas su mišriais baigtinio tūrio / baigtinių elementų priešvėjiniais metodais // Int. J. už skaičių. Metodai skysčiuose. 1998. T. 27. P. 193-206.
50. M. Delanaye, J. A. Essers, Quadratic-reconstruction Finite volume schema for Compressible flows on unstructured adaptive grids // AIAA Journal. 1997. T. 35. P. 631-639.
51. Dervieux A., Steady Eulerio modeliavimas naudojant nestruktūrizuotas akis // VKI Lectures series. 1985. Nr.1884-04.
52. Eisenberg M. A., Malvern L. E., Apie baigtinių elementų integraciją natūraliose koordinatėse // Tarpt. J. Skaičius. Metodai inž. 1973. T. 7. 574-575.
53. A. Fezoui, Netiesioginių priešvėjo schemų klasė Eulerio modeliavimui su nestruktūruotomis akimis//J. Sotr. Fizik. 1989. T. 84. P. 174-206.
54. C. Gallo, G. Manzini, Mišrus baigtinio elemento/ribinio tūrio metodas biologinio skaidymosi transportavimui požeminiame vandenyje // Tarpt. J. už skaičių. Metodai skysčiuose.1998. t. 26. P. 533-556.
55. T. Gallouet, J. P. Vila, Baigtinių tūrių schemos mišraus tipo išsaugojimo dėsniams // SIAM J. Numer. Anal. 1991. T. 28. P. 1548-1573.
56. P. M. Gresho, S. T. Chan, R. L. Lee, G. D. Upson, Modifikuotas baigtinių elementų metodas, skirtas spręsti priklausomybę nuo laiko. Nesuspaudžiamos Navier-Stokes lygtys. 2 dalis. Paraiškos // Tarpt. J. už skaičių. Methods in Fluids, 1984. Vol. 4. P. 619640.
57. A. Grundmann, H. M. Moller, Invariant integration formulas for i-simplex by combinatonal method // SIAM J. Numer. Analinis 1978 t. 15, 282-290 p.
58. W. Hackbusch, Apie pirmos ir antros eilės dėžių schemas // Kompiuterija. 1989. T. 41. P. 277-296.
59. L. P. Hackman, G. D. Raithby, A. B. Strong. Skaitiniai srautų, nukreiptų atgal nukreiptais žingsniais, prognozės // Tarpt. J. už skaičių. Metodai skysčiuose. 1984. T. 4. P. 71 1-724.
60. L. Hallo, C. Ribault, M. Buffat, Netiesioginis mišrus baigtinis tūris-baigtinių elementų metodas 3D turbulentiniams suspaudžiamiems srautams spręsti. J. for Numeric Methods in Fluids, 1997. Vol. 25. P. 1241-1261.
61. F. H. Harlow, J. E. Welch, Nuo laiko priklausomo klampumo nesuspaudžiamo skysčio srauto su laisvu paviršiumi skaitinis skaičiavimas // Phys. Skysčiai. 1965. T. 8. P. 21822189.
62. F. Ilinca, D. Pelletier, A. Garon, An adaptyvus baigtinių elementų metodas dviejų lygčių turbulencijos modeliui sienelės ribotuose srautuose. J. už skaičių. Metodai skysčiuose. 1997. T. 124. P 101-120.
63. E. Issman, G. Degrez, H. Deconinck, Implicit Upwind Residual-Distribution Euler ir Navier-Stokes Solver on Unstructured Meshes // AIAA Journal, 1996. Vol. 34. P. 2021-2028.
64. J. P. Jessee, W. A. Fiveland, „Ląstelės viršūnių algoritmas nesuspaudžiamoms Navier-Stokes lygtims nestačiakampiuose tinkleliuose“, Int. J. už skaičių. Metodai skysčiuose. 1996. T. 23. P. 271-293.
65. Jianguo H., Shitong X., Apie baigtinių tūrio elementų metodą bendroms savaime susietoms elipsinėms problemoms // SIAM .J Skaičius. Anal. 1998. T. 35. P. 1762-1774.
66. M. Lallemand, H. Steve, A. Dervieux, Unstructured Multigridding by volume agglomeration: current status // Computers Fluids, 1992 Vol. 21. P. 397-433.
67. Y. Liu, M. Vinokur, Tiksli daugianarių ir simetrinių kvadratinių formulių integracija per savavališkus daugiakampius tinklelius // J. Comput. Fizik. 1998. T. 140. P. 122-147.
68. D. Marcum, Turbulencijos modeliai nestruktūrizuotų baigtinių elementų skaičiavimams // Tarpt. J.ForNumer. Metodai skysčiuose. 1995, t. 20. P. 803-817.
69. C. Masson, H. I. Saabas, B. R. Baliga, Co-located equal-order control-volume finite element method for two-dimensional axisymmetric incompressible fluid flow // Int J. For Numer. Metodai skysčiuose. 1994. T. 18. P. 1-26.
70. S. Mattiussi, An Analysis of Finite Vol. Baigtinių elementų ir baigtinių skirtumų metodai, naudojant kai kurias algebrinės topologijos sąvokas // J. Comput. Fizik. 1997. T. 133. P. 289-309.
71. D. Mavriplis, Dviejų dimensijų Eulerio lygčių daugiatinklinis sprendimas nestruktūrizuotose trikampėse akyse // AIAA Journal, 1988. Vol 26. P. 824-831.
72. P. R. McHugh, D. A. Knoll, „Nesuspaudžiamų Navier-Stpkes ir energijos lygčių visiškai susieti baigtinio tūrio sprendiniai, naudojant netikslų Niutono metodą“, Int. J. Už skaičių. Metodai skysčiuose. 1994. T. 19. P. 439-455.
73. Y. Murthy, S. Mathur, Periodinis srautas ir šilumos perdavimas naudojant struktūrines akis // Tarpt. J. už skaičių. Metodai skysčiuose. 1997. T. 25. P. 659-677.
74. S. Muzaferija, D. Gosman, Finite-Volume CFD Procedure and Adaptive Error Control Strategy of Grids of Arbitrary Topology // J. Comput. Phys., 1997, t. 138. P. 766-787
75. P. Nithiarasu, O. C. Zienkiewlcz, V. V. K. Satya Sai, K. Morgan, R. Codina, M. Vazquez, Shock capturing viskosities for the general fluid mechanics algorithm // Int. J. už skaičių. Metodai skysčiuose. 1998. T. 28. P. 1325-1353.
76. K. Ohmori, T. Ushijima. Priešsrovinio tipo metodas, taikomas konvekcinės difuzijos lygčių tiesiniam neatitinkančiam baigtinių elementų aproksimavimui // R.A.I.R.O. Anal. Skaičius.
77. D. Pan, J. C. Cheng, Upwind finite volume Navier-Stokes Computations on Uns-structured Triangular Meshes // AIAA Journal, 1993. Vol. 31. P. 1618-1625.
78. S. V. Potapov, Mišrus FE FV algoritmas netiesinėje kietojo kūno dinamikoje // Proc. antrojo stažuotojo. Symp. apie ribotus tomus sudėtingoms programoms. 1999 m. liepos 19-22 d. Duisburgas, Vokietija. - HERMES mokslo leidiniai. Paryžius. 1999. P. 271278.
79. C. Prakash, S. V. Patankar, Kontroliniu tūriu pagrįstas baigtinių elementų metodas, skirtas Navier-Stokes lygtims spręsti naudojant vienodos eilės greičio ir slėgio interpoliaciją //Skaičius. Šilumos perdavimas. 1985. T. 8. P. 259-280.
80. S. Ramadhyani, S. V. Patankar, Puasono lygties sprendimas: Galerkino ir valdymo tūrio metodų palyginimas // Tarpt. J. Skaičius. Metodai inž. 1980. T. 15.1395-1418.
81. Rida S., McKenty F., Meng F. L., Reggio M., A staggered volume control schema for unstructured triangular grids // Int. J. už skaičių. Metodai skysčiuose. 1995. T. 25. P. 697-717.
82. P. L. Roe, apytiksliai Riemann sprendėjai, parametrų vektoriai ir skirtumų schemos //! Sotr. Fizik. 1981. T. 43. P. 357-372.
83. C. Rohde, Upwind Finite volume schemas for silpnai susietoms hiperbolinėms išsaugojimo dėsnių sistemoms 2D // Skaičius. Matematika. 1998. T. 81. P. 85-123.
84. Tony W. H. Sheu, S. K. Wang, S. F. Tsai, Didelės skiriamosios gebos schemos kūrimas daugiamačiai advekcijos-difuzijos lygčiai // J. Sotr. Fizik. 1998. T. 144. P. 1-16.
85. Saad Y., Iteratyvūs retųjų tiesinių sistemų metodai. PSW Publishing Co., Boston, MA, 1995 m.
86. V. V. K. S. Sai, O. C. Zienkiewicz, M. T. Manzari, P. R. M. Lyra, K. Morgan, Bendrasis tikslas versus specialusis algoritmai didelės spartos srautams su smūgiais // Tarpt. J. Skaičius. Meth. Skysčiai. 1998. T. 27. P. 57-80.
87. J. L. Sohn, Evaluation of FIDAP on some classic laminar and turbulent benchmarks // Int. J. už skaičių. Metodai skysčiuose. 1988. T. 8. P. 1469-1490.
88. In Stoufflet, Investigation of generalized flux vektori splitting for suspaudžiamiems srautams ant trikampių akių // Int. J. už skaičių. Metodai skysčiuose. 1995. T. 20. P. 1047-1059.
89. B. Stouflette. J. Periaux, F. Fezoui, A. Dervieux, Skaitmeninis 3-D hipergarsinių Eulerio srautų modeliavimas aplink kosmines transporto priemones naudojant pritaikytus baigtinius elementus // AIAA Paper 87-0560.
90. C. Taylor, P. Hood, Navier-Stokes lygčių skaitmeninis sprendimas baigtinių elementų technika // Kompiuteriai ir skysčiai. 1973. T. 1. P. 73-100.
91. Thomadakis M, Leschziner M., Slėgio korekcijos metodas nesuspaudžiamų klampių srautų tirpimui ant nestruktūrizuotų grotelių // Int.J. Skaitmeniniams skysčių metodams. -1996 m. t. 22 P 581-601.
92. A. K. Verma, V. Eswaran, Overlapping volume control approach for convection-diffusion problems // Int. J. už skaičių. Metodai skysčiuose. 1996. T. 23. P. 865-882.
93. M. M. T. Wang, T. W. H. Sheu, Apie kompaktišką mišrios eilės baigtinį elementą trimačių nesuspaudžiamų Navier-Stokes lygčių sprendimui // Tarpt. J. už skaičių. Metodai skysčiuose. 1997. T. 25. P. 513-522.
94. M. M. T. Wang, T. W. H. Sheu, Navier-Stokes lygčių laisvosios ribinės sąlygos įgyvendinimas // Tarpt. J. Skaičius. Methods Heat and Fluid Flow, 1997. T. 7. P. 95-111.
95. D. Winterscheidt, K. S. Surana, p-Versija mažiausių kvadratų baigtinių elementų formuluotė dvimačiam nesuspaudžiamam skysčio srautui // Int. J. Skaičius. Meth. Fluids, 1994. T. 18. P. 43-69.
96. A. M. Winslow, Kvazilinijinės Puasono lygties skaitinis sprendimas nevienodoje trikampio tinklelyje, J. Comput. Fizik. 1967. T. 2. 149-172.
97. A. Younesas, R. Mose. P. Ackereris. G. Chavent, Nauja mišriųjų baigtinių elementų metodo formuluotė, skirta elipsiniam ir paraboliniam PDE išspręsti trikampiais elementais // J. Comput. Phys., 1999. T. 149. P. 148-167.
98. P.J. Zwart, G. D. Raithby, M. J. Raw, Integruotas erdvės ir laiko baigtinio tūrio metodas ir jo taikymas judančių ribų problemoms // J. Comput. Fizik. 1999. T. 154. P. 497-519.
99. O. C. Zienkiewiczius, The Finite Element Method in Engineering Science // McGraw-Hill London. 1971 m.
100. O.C. Zienkiewicz, R. Codina, Bendras suspaudžiamo ir nesuspaudžiamo srauto algoritmas. 1 dalis. Suskaidyta charakteristika pagrįsta schema // Tarpt. J. Skaičius. Meth. Skysčiai. 1995. T. 20. P. 869-885.
101. S. M. Rhie ir W. L. Chow, Turbulentinio srauto, einančio pro izoliuotą aerodinaminį sparną su galinių kraštų atskyrimu, skaitmeninis tyrimas // AIAA dokumentas Nr. 82-0998. 1982 m.
102. R. I. Issa, Netiesiogiai diskretuotų skysčio srauto lygčių sprendimas operatoriaus padalijimu//J. Comput. Fizik. t. 62. P. 40-65.1985.
103. J. Kim, S. J. Kline, J. P. Johnston, Investigation of a Reattaching Turbulent Shear Layer: Flow Over a Backward-Facing Step, Journal of Fluids Eng., Vol. 102, p. 302-308.117. http//www.ict.nsc.ru/linpar
Atkreipkite dėmesį, kad aukščiau pateikti moksliniai tekstai yra paskelbti tik informaciniais tikslais ir buvo gauti naudojant originalų disertacijos teksto atpažinimą (OCR). Todėl juose gali būti klaidų, susijusių su netobulais atpažinimo algoritmais. Mūsų pristatomuose disertacijų ir santraukų PDF failuose tokių klaidų nėra.
Prieš kurį laiką ieškojau operacijų ir procesų, vykstančių OpenFOAM skaitmeninio modeliavimo bibliotekoje, aprašymo. Radau daug abstrakčių baigtinio tūrio metodo veikimo aprašymų, klasikinių skirtumų schemų, įvairių fizikinių lygčių. Norėjau sužinoti išsamiau - iš kur atsirado šios reikšmės tokiame ir tokiame išvesties faile esant tokiai ir tokiai iteracijai, kokios išraiškos yra už tam tikrų parametrų fvSchemes, fvSolution nustatymų failuose?
Tiems, kurie taip pat domisi - šis straipsnis. Tie, kurie gerai išmano OpenFOAM ar jame įdiegtus metodus – apie rastas klaidas ir netikslumus rašykite asmenine žinute.
Habré svetainėje jau buvo keli straipsniai apie OpenFOAM:
Todėl nesigilinsiu į tai, kad tai „atvira (GPL) skaitmeninio modeliavimo platforma, skirta modeliavimui, susijusiam su dalinių diferencialinių lygčių sprendimu baigtinio tūrio metodu, ir yra plačiai naudojama sprendžiant kontinuumo mechanikos problemas“.
Šiandien aš naudosiu paprastą pavyzdį, kad apibūdinčiau operacijas, kurios vyksta atliekant skaičiavimus OpenFOAM.
Taigi, atsižvelgiant į geometriją - kubas, kurio kraštinė yra 1 metras:
Mes susiduriame su užduotimi modeliuoti tam tikro skaliarinio lauko (temperatūros, medžiagos kiekio) srauto sklidimą, kurį pateikia tokia transporto lygtis (1) kūno tūrio viduje.
(1) ![]() ,
,
Kai skaliarinis dydis, pavyzdžiui, išreiškia temperatūrą [K] arba tam tikros medžiagos koncentraciją ir išreiškia medžiagos perdavimą, masės srautą [kg/s].
Ši lygtis, pavyzdžiui, naudojama šilumos sklidimui modeliuoti ![]() ,
,
kur k yra šilumos laidumas ir temperatūra [K].
Divergencijos operatorius iš tikrųjų yra
operatorius .
Leiskite jums priminti, kad yra nabla operatorius (Hamilton operatorius), kuris parašytas taip: ![]() ,
,
Kur i, j, k yra vienetiniai vektoriai.
Jei nabla operatorių skaliariai padauginsime iš vektoriaus dydžio, gausime šio vektoriaus divergenciją:
„Fizikos požiūriu vektorinio lauko divergencija yra rodiklis, kiek tam tikras erdvės taškas yra šio lauko šaltinis arba grimzlė“.
Jei nabla operatorių padauginsite iš skaliro, gausite to skaliro gradientą:
Gradientas rodo skaliarinio dydžio padidėjimą arba sumažėjimą tam tikra kryptimi.
Problemos ribinės sąlygos yra tokios: yra įvesties paviršius, išėjimo paviršius, o likę paviršiai yra lygios sienos.

Kubo tūrio padalijimas į baigtinius tūrius
Mūsų tinklelis bus labai paprastas – kubą padaliname į 5 lygias ląsteles išilgai Z ašies.
Daug formulių
Baigtinio tūrio metodas numato, kad (1) integralioje formoje (2) bus patenkintas kiekvienam baigtiniam tūriui.
(2)![]() ,
,
Kur yra galutinio tūrio geometrinis centras.
Galutinio tūrio centras

Supaprastinkime ir paverskime pirmąjį išraiškos (2) narį taip:
(2.1) (HJ-3.12)*
Kaip matote, padarėme prielaidą, kad skaliarinis dydis baigtinio tūrio viduje kinta tiesiškai, o kiekio vertę tam tikru tašku baigtinio tūrio viduje galima apskaičiuoti taip:
Norėdami supaprastinti antrąjį išraiškos narį (2), naudojame apibendrintą Gauso-Ostrogradskio teoremą: vektoriaus lauko divergencijos per tūrį integralas yra lygus vektoriaus srautui per paviršių, ribojantį duotą tūrį. Žmonių kalba, „visų srautų į/iš baigtinio tūrio suma yra lygi srautų per šio baigtinio tūrio paviršius sumai“:
(2.3)![]() ,
,
Kur yra uždaras paviršius, ribojantis tūrį,
- vektorius, nukreiptas išilgai normalios nuo tūrio.
Vektorius S

Atsižvelgiant į tai, kad baigtinį tūrį riboja plokščių paviršių aibė, išraiška (2.3) gali būti transformuota į viso paviršiaus integralų sumą:
(2.4) (HJ-3.13)
,
Kur išreiškia kintamojo vertę veido centre,
- ploto vektorius, išeinantis iš veido centro, nukreiptas nuo ląstelės (lokaliai), nuo mažesnio indekso ląstelės į aukštesnio indekso ląstelę (globalus).
Šiek tiek daugiau apie vektorių S
Kad nebūtų du kartus išsaugoti tie patys vektoriaus parametrai, nes Akivaizdu, kad dviejų gretimų ląstelių normalus vektorius iki krašto tarp ląstelių, nukreiptas nuo ląstelės centro, skirsis tik krypties ženklu. Todėl tarp krašto ir ląstelės buvo sukurti savininko ir kaimyno santykiai. Jei ploto vektorius (globali, teigiama kryptis nuo ląstelės su mažesniu indeksu į ląstelę su didesniu indeksu) rodo IŠ ląstelės centro, toks ryšys tarp ląstelės ir vektoriaus, o tiksliau tarp ląstelės ir veidas, žymimas savininkas). Jei šis vektorius rodo atitinkamos ląstelės viduje, tada kaimynas. Kryptis turi įtakos vertės ženklui (+ savininkui ir - kaimynui) ir tai svarbu sumuojant, žr. toliau.
Apie skirtumų schemas
Vertė veido centre apskaičiuojama pagal gretimų ląstelių centrų reikšmes - šis išraiškos metodas vadinamas skirtumo schema. OpenFOAM skirtumo schemos tipas nurodytas faile /system/fvSchemes:DivSchemes (numatytasis nėra; div(phi,psi) Gauso tiesinis;)
Gausas- reiškia, kad pasirinkta centrinio skirtumo schema;
linijinis- reiškia, kad interpoliacija iš ląstelių centrų į veidų centrus vyks tiesiškai.

Tarkime, kad mūsų skaliarinis dydis kinta tiesiškai baigtinio tūrio viduje nuo centro iki kraštų. Tada apytikslė vertė veido centre bus apskaičiuojama pagal formulę:
Kur yra svoriai ir apskaičiuojami kaip
Kur yra ląstelių tūriai.
Iškreiptų langelių atvejais yra sudėtingesnės formulės apytiksliesiems svoriams apskaičiuoti.
Taigi, phi_f reikšmės langelio kraštų centruose apskaičiuojamos pagal vertes ląstelių centruose. Gradiento reikšmės grad(phi) apskaičiuojamos remiantis phi_f reikšmėmis.
Ir visą šį algoritmą galima pavaizduoti šio pseudokodo forma.
1. Deklaruojame baigtinių tūrių gradientų masyvą, inicijuojame jį nuliais 2. Einame per visus vidinius paviršius (kurie nėra ribos) > Apskaičiuojame flux_f = phi_f*S_f. Apskaičiuokite phi_f reikšmes pagal phi reikšmes langelio centais > Pridėkite flux_f prie savininko elemento gradiento ir -flux_f prie kaimyninio elemento gradiento 3. Pakartokite per visus kraštinius > Apskaičiuoti flux_f = phi_f*S_f > Pridėkite flux_f prie savininko elemento gradiento (kaimynas -ribiniai paviršiai neturi elementų) 4. Pereikime per visus elementus > Padalinkite gautą gradiento sumą iš elemento tūrio
Laiko atranka

Atsižvelgiant į (2.1) ir (2.4), (2) išraiška yra tokia:
(3)
Pagal baigtinio tūrio metodą atliekama laiko diskretizacija ir išraiška (3) rašoma taip:
(4)
Integruokime (4):
(4.1)![]()
Padalinkime kairę ir dešinę puses į:
(5)
Duomenys imties matricai
Dabar galime gauti tiesinių lygčių sistemą kiekvienam baigtiniam tūriui.Žemiau yra tinklelio mazgų, kuriuos naudosime, numeracija. 
Mazgo koordinatės saugomos /constant/polyMesh/points
24
((0 0 0)
(1 0 0)
(0 1 0)
(1 1 0)
(0 0 0.2)
(1 0 0.2)
(0 1 0.2)
(1 1 0.2)
(0 0 0.4)
(1 0 0.4)
(0 1 0.4)
(1 1 0.4)
(0 0 0.6)
(1 0 0.6)
(0 1 0.6)
(1 1 0.6)
(0 0 0.8)
(1 0 0.8)
(0 1 0.8)
(1 1 0.8)
(0 0 1)
(1 0 1)
(0 1 1)
(1 1 1))
Ląstelių centrų mazgų numeracija (50, 51 – kraštinių paviršių centrai): 
Veido centro mazgų numeracija: 
Elementų tūriai:
Interpoliacijos koeficientai, reikalingi langelių paviršių reikšmėms apskaičiuoti. Indeksas „e“ reiškia „dešinį langelio kraštą“. Tiesiai atsižvelgiant į vaizdą, kaip parodyta paveikslėlyje „Ląstelių mazgų centrų numeracija“:
Atrankos matricos formavimas
Jei P = 0.
Išraiška (5), apibūdinanti kiekio elgesį

Bus transformuota į linijinių algebrinių lygčių sistemą, kurios kiekviena iš šių formų:
Arba pagal taškų indeksus ant veidų
Ir visi srautai į / iš ląstelės gali būti išreikšti suma

Kur, pavyzdžiui, srauto tiesinimo koeficientas langelio E centre,
- srauto tiesinimo koeficientas veido centre,
- netiesinė dalis (pavyzdžiui, konstanta).
Pagal veidų numeraciją išraiška bus tokia: 
Atsižvelgiant į elemento P_0 ribines sąlygas, tiesinė algebrinė lygtis gali būti pavaizduota kaip
...pakeisti anksčiau gautus koeficientus...

Srautas iš įleidimo angos"a nukreipiamas į ląstelę, todėl turi neigiamą ženklą.
Kadangi mūsų kontrolinė išraiška, be difuzijos termino, turime ir laiko terminą, tačiau galutinė lygtis atrodo taip
Jei P = 1.
Jei P = 4.
Tiesinių algebrinių lygčių sistema (SLAE) gali būti pavaizduota matricos forma kaip
A(i,j) === 40,5 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40 0,5 0 0 0 -0,5 40,5
Psi = matmenys; internalField nevienodas sąrašas
Remiantis tuo, gaunamos vektoriaus reikšmės
Tada vektorius pakeičiamas SLAE ir įvyksta nauja vektoriaus skaičiavimo iteracija.
Ir taip toliau, kol neatitikimas pasiekia reikiamas ribas.