Построение сеток для метода конечных объемов. Метод конечных объёмов. Разбиение объема куба на конечные объемы
Преимущество этого метода заключается в том, что в его основе лежат законы сохранения. Поэтому, в отличие от метода конечных разностей, метод контрольного объема обеспечивает консервативность численной схемы, что позволяет даже на относительно грубых сетках получать приемлемые по точности решения .
Основная идея метода достаточно проста и легко поддается физической интерпретации. При дискретизации уравнений Навье-Стокса, осредненных по Рейнольдсу, расчетная область разбивается на большое количество непересекающихся элементарных объемов, таким образом, чтобы каждый объем содержал только одну расчетную (узловую) точку. Совокупность элементарных объемов называется расчетной сеткой. Ячейки сетки могут иметь различную форму. Наиболее часто используются шестигранники (гексаэдры) и четырехгранники (тетраэдры). Метод контрольного объема позволяет использовать ячейки с произвольным числом граней (пирамиды, призмы, сложные многогранники и т. п.).
Решение системы уравнений (1)–(18) представляется в виде набора значений искомых параметров в центрах этих объемов. Например, если разбить объем помещения на 1000 отдельных элементарных объемов (ячеек), то в результате решения мы будем иметь 1000 значений температуры, скорости, давления и т. д. На рис. 2 представлен фрагмент расчетной области. Ячейки пронумерованы индексами i, j, k .
Рис. 2. Фрагмент расчетной области
Интегрирование дифференциальных уравнений производится по каждому элементарному объему. Интегралы вычисляются с использованием интерполяционных формул, при помощи которых определяют значения искомых переменных между расчетными точками. В результате получают дискретный аналог исходных уравнений в узловых точках, который отражает закон сохранения изучаемых переменных в каждом конечном объеме.
Следует отметить, что в большинстве современных расчетных гидродинамических пакетах таких как «STAR-CD», «FLUENT», «CFX» и многих других для дискретизации уравнений модели реализован метод контрольного объема.
Расчетные сетки
Процесс построения сетки относится к ключевым моментам проведения численного эксперимента. Выбор и построение адекватной для рассматриваемой задачи расчетной сетки является достаточно сложной и трудоемкой процедурой. Рациональный выбор сетки может значительно упростить численное решение задачи.

Рис. 3. Конфигурации ячеек сеток
Ячейки сетки могут иметь разную форму (рис. 3) и размеры, наилучшим образом подходящие для решения конкретной задачи. Наиболее простой вид сетки, когда ячейки одинаковы и имеют кубическую форму.
Как правило, вблизи твердых поверхностей сетка сгущается, т. е. ячейки имеют меньший размер по нормали к поверхности. Это делается для повышения точности расчетов в тех областях, где градиенты потоков изучаемых параметров изменяются быстрее, например, в пограничном слое.
Повысить точность расчетов и уменьшить ошибку аппроксимации можно 2 способами:
· повышением порядка точности дискретизации;
· уменьшением шага по сетке .
При решении нестационарных задач размеры ячеек Δx и шаг интегрирования по времени Δt связанны условием КФЛ (Куранта-Фридрихса-Леви):  , u
– скорость.
, u
– скорость.
Универсальные вычислительные программы, применяемые в настоящее время в инженерной практике, позволяют работать на произвольных неструктурированных сетках с использованием сильно скошенных элементов. При этом порядок точности дискретизации, как правило, не превышает второго. Для получения качественного решения необходимо строить расчетные сетки с малым шагом.
В пакете STAR-CCM осуществлен переход на использование полиэдральных ячеек (похожих на футбольный мяч), что позволяет за счет объединения ячеек исключить появление сильно скошенных ячеек.
Основное преимущество неструктурированных сеток по сравнению с регулярными – заключается в большей гибкости при дискретизации физической области сложной формы. При этом ячейки сетки должны иметь соизмеримые объемы или площади и не должны пересекаться. Однако к недостаткам такого типа сеток относится увеличение размерности сетки. Как показывает практика, для одного и того же объекта неструктурированная сетка при ее правильном построении имеет примерно в два раза больше ячеек, чем структурированная, что естественно приводит к увеличению времени счета по отношению к регулярным сеткам. Однако во многих случаях неструктурированные сетки являются единственно возможным вариантом построения из-за сложности геометрии объекта. Кроме того, при рациональном выборе алгоритма построения сетки время, затрачиваемое на построение неструктурированной сетки, оказывается существенно меньше, чем время построения структурированной (блочно-структурированной) сетки. В результате суммарное время, затраченное на решение задачи (включая время построения сетки и время счета), может при использовании неструктурированных сеток оказаться намного меньше, чем в случае структурированных.
Определение требуемой размерности сетки, само по себе, является весьма сложной задачей. Универсальный способ, которым следует руководствоваться при выборе размерности сетки, сводится к тому, что получаемое решение не должно изменяться при увеличении количества ячеек (сеточная сходимость).
Для типовых задач проведение исследования сеточной сходимости не является обязательным, так как можно ориентироваться на полученные ранее результаты. При переходе к изучению нового типа задач следует в обязательном порядке выполнить исследование сеточной сходимости и определелить требования к расчетной сетке.
Отметим, что при решении реальных задач вентиляции и кондиционирования воздуха характерное количество ячеек составляет, как правило, от 500 тысяч до 3 – 4 млн. в зависимости от геометрической сложности объекта, набора искомых параметров и специфики задачи. При этом время счета на кластере, состоящем, например из 24 ядер, может доходить до недели, а при решении нестационарных задач – до нескольких недель.
Пакет STAR-CCM+ включает в себя модуль для построения расчетных сеток. Существуют также отдельные пакеты для построения сеток, например, широко используемая – ANSYS, ICEM CFD (ICEM). Построенные во внешних пакетах сетки могут быть импортированы в пакет STAR-CCM+.
Глава 1. Методы дискретизации систем законов сохранения.
1.1. Технологические принципы методов дискретизации начально-краевых задач, использующих конечноэлементные пространства.
1.1.1. Методы конечных элементов.
1.1.2. Методы конечных объемов.
1.2. Противопотоковые схемы на симплициальных сетках.
1.3. Методы решения стационарной системы уравнений Навье-Стокса.
Гпава 2. Построение дискретных аналогов конвективно-диффузионно-реакционных уравнений методом конечных объемов
2.1. МКО/КЭ дискретизация задач конвективно-диффузионного типа.
2.1.1. Триангуляция и способ построения двойственной сетки.
2.1.2. Интегральная форма законов сохранения.
2.1.3. Аппроксимация диффузионных потоков и расчет матрицы жесткости МКО/КЭ.
2.1.4. Аппроксимация источниковых членов.
2.1.5. Расчет матрицы массы МКО/КЭ.
2.1.6. Учет граничных условий.
2.2. Построение многомерных противопотоковых схем на симплициальных сетках.
2.2.1. Расчет конвективных локальных матриц.
2.2.2. Схемы со взвешиванием потоков массы.
2.2.3. Модификация экспоненциальных схем.
2.2.4. Некоторые свойства противопотоковых схем и принципы их построения.
2.2.5. Аналог экспоненциальной схемы для схем с расчетом неизвестных в центрах ячеек.
2.3. Новые классы интегральных формул МКО.
2.3.1. Интегрирование одночленов барицентрических координат.
2.3.2. О возможных сочетаниях полиномиальных представлений.
2.3.3. О повышении порядка интерполяционных полиномов локального представления решения.
2.4.4. Использование несогласованных конечных элементов.
2.4. Поэлементная сборка глобальных матриц
Гпава 3. Моделирование поля течения вязких несжимаемых сред.
3.1. Математическая модель.
3.2. Интегральная форма законов сохранения.
3.3. Учет взаимосвязи полей скорости-давления.
3.3.1. Интерполяция Рая-Чоу для расчета потоков массы.
3.3.2. Дискретизация уравнения неразрывности.
3.3.3. Учет границ с ненулевым массовым расходом.
3.3.4. Общая итерационная схема 1.
3.4. Ускорение сходимости итерационных схем.
3.4.1. Коррекция полей давления и скорости
3.4.2. Общая итерационная схема II.
3.5. Решение систем линейных алгебраических уравнений.
Гпава 4. Численные эксперименты.
4.1. Анализ устойчивости на решениях погранслойного типа.
4.2. Разгонное течение в круглой трубе.
4.3. Течение в начальном участке гладкого канала.
4.4. Ламинарное истечение струи из точечного сопла (струя-источник)
4.5. Ламинарное течение за плоским асимметричным обратным уступом
4.5.1. Расчет с использованием различных противопотоковых схем
4.5.2. Входной эффект при расчете течений за обратным уступом с использованием МКО/КЭ на симплициальных сетках.
4.5.3. Сравнение различных способов решения систем линейных алгебраических уравнений.
Рекомендованный список диссертаций
Моделирование внутренних течений вязкой несжимаемой жидкости методом конечных элементов с использованием противопотоковых схем 2007 год, кандидат физико-математических наук Гобыш, Альбина Владимировна
Численные схемы на основе конечно-объёмных/конечно-элементных аппроксимаций для решения задач длинноволновой гидродинамики 2004 год, кандидат физико-математических наук Стыврин, Андрей Вадимович
Параллельные технологии решения краевых задач 2005 год, доктор физико-математических наук Василевский, Юрий Викторович
Метод конечных объемов для задачи конвекции-диффузии и моделей двухфазных течений 2010 год, кандидат физико-математических наук Никитин, Кирилл Дмитриевич
Трехмерное моделирование процессов переноса примесей в пористых средах сложной структуры 2007 год, кандидат физико-математических наук Капырин, Иван Викторович
Введение диссертации (часть автореферата) на тему «Технологии метода конечных объемов/конечных элементов на симплициальных сетках для задач конвективно-диффузионного типа»
Численное решение задач математической физики является одним из основных методов исследования реальных явлений. Совместное использование вычислительного и физического экспериментов при анализе какого-либо явления позволяет, с одной стороны, уменьшить количество дорогостоящих экспериментальных измерений, а с другой стороны - провести верификацию и усовершенствование математических моделей.
С увеличением быстродействия вычислительных систем все новые требования предъявляются к численным методам решения задач математической физики. Разработка и усовершенствование современных методов дискретизации законов сохранения, предоставляющих возможность моделирования все новых классов задач и получение существенно лучших результатов при решении известных, является важным направлением исследований.
Современные вычислительные алгоритмы должны предоставлять возможность наиболее точного описания областей со сложной геометрией. Это возможно с использованием неортогональных и неструктурированных сеток. По сравнению с произвольными неортогональными сетками для неструктурированных симплициальных сеток (триангуляция в двумерном случае и разбиение на тетраэдры в трехмерном) легче реализуются локальные сгущения (например, за обратным уступом, в зоне внезапного сужения, в окрестности точки присоединения), а также, если это необходимо, адаптация расчетной сетки в зависимости от поведения решения. Таким образом, даже при дискретизации законов сохранения в геометрически простых областях, которые могут быть точно представлены совокупностью прямоугольных элементов, неструктурированные симплициальные сетки имеют ряд преимуществ. Несмотря на очевидные достоинства неструктурированных сеток при аппроксимации произвольных областей и возможности автоматического построения симплициальных разбиений, они практически не использовались в вычислительной гидродинамике, и лишь в последние 15 лет приобретают все большую популярность. Согласно свидетельству Б. Стоуффлетга и др. , причиной тому является резко возрастающее при переходе к неструктурированным подходам время расчетов. Дело в том, что положение ненулевых элементов в матрицах дискретных аналогов зависит от смежности узлов сетки и произвольно, матрицы хранятся с использованием универсальных форматов и структур данных. Гораздо более «дорогостоящими» становятся операции умножения разреженной матрицы на вектор и неполной факторизации. В то же самое время системы уравнений вычислительной гидродинамики - взаимосвязанные нелинейные системы уравнений, неявные схемы решения которых имеют многоуровневый итерационный характер, так что на каждой из «глобальных» итераций необходимо решить несколько систем линейных алгебраических уравнений. Именно с появлением мощных вычислительных систем, а также благодаря развитию адаптивных и многосеточных методов стало возможно использование неструктурированных сеток и соответствующих схем пространственной дискретизации для моделирования гидрогазодинамических процессов.
Наиболее распространенным методом дискретизации в неструктурированном случае является метод конечных элементов (МКЭ) . Отметим такие достоинства метода, как сохранение симметричной природы самосопряженной части дифференциальных операторов в их дискретных аналогах (это достигается специальным выбором пространства тестовых функций совпадающим с пространством пробных функций), возможность повышения точности аппроксимации за счет повышения степени интерполяционных полиномов локального представления решения (т. н.р и h-p версии МКЭ, ), естественный учет граничных условий второго и третьего рода. Метод конечных элементов имеет установившуюся технологическую основу, в частности
Способы аппроксимации внутренних произведений в предположении о кусочно-полиномиальном представлении решения и параметров краевой задачи, а именно: использование разложения по базису соответствующего конечноэлементного пространства, классы интегральных формул, позволяющие точно интегрировать произвольные произведения базисных функций по элементам разбиения и ребрам (граням) элементов,
Стандартный аппарат интерполяции.
Технологии метода позволяют просто и единообразно строить дискретные аналоги начально-краевых задач, с различными типами граничных условий в предположении об определенной степени гладкости решения и кусочно-полиномиальном поведении коэффициентов уравнений и краевых условий , .
В ряде приложений, таких, как моделирование сверхзвуковых и трансзвуковых течений газов, расчеты с использованием моделей мелкой воды, очень важна локальная консервативность схем, используемых для дискретизации законов сохранения. Метод конечных элементов не позволяет с удовлетворительной точностью отследить особенности возникающих разрывных решений , и традиционным подходом к решению таких задач является метод конечных объемов. При дискретизации системы законов сохранения методом конечных объемов расчетная область аппроксимируется множеством открытых конечных объемов, затем исследователь делает «шаг назад», переходя к интегральной форме исходной системы уравнений; с использованием формулы Остроградского-Гаусса от интегрирования по объему переходят к интегралу по границе, так что способ аппроксимации потоков через грани конечных объемов полностью определяет вычислительную схему. Согласно монографии С. Патанкара , "для большинства исследователей, работающих в области гидродинамики и теплообмена, конечно-элементный метод все еще кажется окутанным покровом таинственности. Вариационная формулировка и даже метод Галеркина не поддаются простой физической интерпретации". В то же самое время конечнообъемные схемы имеют определенный физический смысл баланса потоков и источниковых членов в каждом из конечных объемов, аппроксимирующих расчетную область, что делает метод конечных объемов более привлекательным. «Простота» МКО является одной из причин отсутствия общей технологической основы метода.
Итак, к преимуществам классического варианта МКО (метода конечных объемов/конечных разностей, FVDM) относят локальную консервативность дискретных схем, большую простоту и наглядность, возможность естественного учета граничных условий второго рода . Кроме того, в случае решения задач с преобладанием конвекции, упрощается реализация противопотоковых схем, поскольку потоки через грани конечных объемов являются одновременно и анализируемыми, и аппроксимируемыми величинами.
Попытки систематизации конечнообъемных аппроксимаций привели к частичному соединению технологий МКЭ и принципа интегрирования по конечным объемам; самые ранние из них восходят к работам Б. Р. Балиги, К. Пракаша и С. Патанкара и известны как методы CVFEM (control-volume-based finite element methods), далее - методы конечных объемов/конечных элементов (МКО/КЭ) . Авторы метода преследовали цель построения консервативных схем метода конечных объемов, использующих одно из основных преимуществ МКЭ - возможность аппроксимации сложных геометрий с использованием неструктурированных сеток. Функции профиля в данном классе методов "носят вспомогательный характер" , принадлежность решения конечноэлементным пространствам не подчеркивается. В качестве двойственного разбиения используются барицентрические множества.
Впервые проблема отсутствия универсальных технологических принципов метода конечных объемов/конечных разностей (МКО/КР, FVDM), обсуждается в работе 3. Кая "О методе конечных объемов/элементов" . Автор обращает внимание читателя на "бессистемность метода конечных объемов/конечных разностей"; при аппроксимации систем законов сохранения методом конечных объемов/конечных разностей в рамках одной работы могут использоваться апроксимации различных классов, что существенно усложняет анализ сходимости подобных схем. Предлагается решение данной проблемы -совместное использование идей метода конечных элементов (поиск решения в некотором конечноэлементном пространстве и использование кусочно-полиномиального поведения решения для вычисления потоков) и интегральной формы законов сохранения . Таким образом, методы конечных объемов/элементов (МКО/Э, "бокс-методы", FVE) возникли при попытке создания "более систематизированных конечнообъемных технологий". Отсутствие общих технологических принципов методов конечных объемов/конечных разностей отмечается также в работах Я. JI. Гурьевой и В. П. Ильина .
Методы конечных объемов/элементов (FVE) и методы конечных объемов/конечных элементов (CVFEM) используют согласованные конечноэлементные пространства линейных на симплексах функций и принадлежат классу методов конечных объемов с расчетом переменных в узлах (cell-vertex finite volume schemes), рис. 1, a.
Ряд схем вычислительной гидродинамики (моделирование вязких несжимаемых течений) использует несогласованные конеч ноэлементные пространства, в частности, пространство Крузея-Равьяра линейных на элементах, непрерывных в центрах ребер пробных функций . Методы конечных объемов, использующие несогласованные конечноэлементные пространства, были предложены С. Чоем и Д. Кваком , исследованы в ряде работ других авторов (т. н. методы подобъемов, covolume method) и являются схемами с расчетом неизвестных в центрах ребер ( Наиболее распространенными при решении задач газовой динамики и моделировании антропогенных катастроф с использованием уравнений мелкой воды являются схемы с расчетом неизвестных в центрах ячеек (cell-centered finite volume schemes) , рис. 1, е. Их популярность обусловлена тем, что в случае расчета неизвестных в центроидах большинство схем газовой динамики (схемы С. К. Годунова, TVD-схемы) могут быть перенесены на неструктурированные сетки без принципиальных технологических изменений. о а в Рис.1. Расположение расчетных точек по отношению к узлам сетки КЭ. В данной работе преимущественно рассматриваются классы методов конечных объемов с расчетом неизвестных в узлах триангуляции (МКО/Э, МКО/КЭ) и центрах ребер (методы подобъемов), в дальнейшем будем также говорить "методы конечных объемов, использующие конечноэлементные пространства". Данные классы методов, согласно ряду исследований (, ), для задач конвекции-диффузии дают лучшие приближения к решению, чем методы с расчетом неизвестных в центрах ячеек. Одна из основных причин состоит в том, что для перечисленных выше методов сохраняется непрерывность первых производных пробных функций на элементах двойственной сетки . Эффективным подходом к решению задач с преобладанием конвекции является использование метода Галеркина с симметричными тестовыми функциями для самосопряженной части дифференциальных операторов и проти-вопотоковых схем МКО - для несимметричной их части, т. н. смешанных методов конечных элементов/объемов (МКЭ/О, MEV, mixed element/volume method) . Диссертационная работа посвящена, в частности, усовершенствованию технологий метода конечных объемов для указанных классов методов (МКО/Э, МКО/КЭ, МКЭ/О, методы подобъемов). В настоящий момент данные методы не обладают устоявшимися технологиями учета кусочно-полиномиального полиномиального поведения решения, источниковых членов и коэффициентов переноса. Можно перечислить следующие причины несовершенства аппарата точного интегрирования полиномов в методах конечных объемов, использующих конечноэлементные пространства: 1. В отличие от метода конечных элементов, метод конечных объемов не имеет р-версии, поскольку с введением дополнительных узлов и нескольких типов двойственных сеток нарушается локальная консервативность ряда переменных системы законов сохранения по отношению к "чужим" конечным объемам. Таким образом, аппроксимации ограничены конечно-элементными пространствами младших порядков. 2. По сравнению с методом конечных элементов, для методов конечных объемов характерна большая свобода в выборе пространств тестовых функций, которые в этом случае оказываются связанными с расположением точек расчета неизвестных по отношению к узлам дискретизации (схемы с расположением неизвестных в узлах, серединах ребер, центроидах симплексов) и способом построения двойственной сетки (использование барицентрических, ортоцентрических, циркумцентрических множеств). В сочетании с возможностью использования совмещённых (collocated) или разнесённых (staggered) сеток это дает все многообразие существующих схем МКО в каждом из приложений. Для МКО-методов дискретизации законов сохранения, использующих конеч-ноэлементные пространства, тщательный выбор этих пространств для решения, коэффициентов уравнений и источниковых членов отчасти теряет смысл, если метод не обладает развитыми средствами учета кусочно-полиномиальных представлений, в частности, аппаратом точного интегрирования полиномов по элементам двойственной сетки, подобластям элементов и отрезкам приграничных ребер. Как следствие, результаты расчетов по построенным схемам должны рассматриваться с точки зрения эффектов численного интегрирования, с учетом различных способов их реализации; существенно усложняется сравнение результатов исследований с работами других авторов и т.д. Итак, настоящая работа посвящена пересмотру существующих МКО/МКЭ-технологий построения дискретных аналогов задач конвективно-диффузионного типа. Технология учета кусочно-полиномиального представления решения, коэффициентов уравнения и входящих в граничные условия, а также источниковых членов в методах конечных объемов, использующих конечноэлементные пространства, должна удовлетворять следующим требованиям: 1) допускать произвольные сочетания полиномиальных представлений коэффициентов и решения на элементах разбиения, а также повышение степени интерполяционных полиномов локального представления решения; 2) использовать единые принципы аппроксимации при расчете вкладов элементов, соответствующих различным членам уравнения (диффузионных, конвективных, реакционных слагаемых, источниковых членов), а также вкладов от ребер, аппроксимирующих части границ с заданными на них различного типа граничными условиями; 3) допускать однородное обобщение на трехмерный случай; 4) учитывать опыт хорошо разработанных конечноэлементных технологий, в частности, использование разложения по базису конечноэлементных пространств и преимущества точного интегрирования кусочно-полиномиальных представлений решения и коэффициентов переноса; 5) доставлять единую технологическую основу смешанным аппроксимациям МКЭ/О, использующим два множества тестовых функций - конечнообъ-емных и конечноэлементных - для аппроксимации одного уравнения; 6) принципы технологии должны оставаться неизменными при переходе от использования согласованных конечноэлементных пространств (методы конечных объемов/конечных элементов с расчетом неизвестных в узлах) к использованию несогласованных конечных элементов (методы с расчетом неизвестных в центрах ребер триангуляции); 7) технология может быть использована при аппроксимации различных классов физических задач. Из существующих технологий методов конечных объемов, использующих ко-нечноэлементные пространства (методы конечных объемов/элементов (FVE), методы конечных объемов/конечных элементов (CVFEM), методы подобъемов (covolume methods), смешанные методы объемов/элементов (MEV)), ни одна не удовлетворяет перечисленным выше требованиям. Таким образом, создание новых технологий для данных классов методов, использующих симплициаль-ные разбиения и барицентрические множества в качестве двойственных, представляется актуальной темой исследования. В случае существенного преобладания конвекции, сравнение различных схем МКО-дискретизации, а также сравнение расчетов по методу конечных элементов и методу конечных объемов фактически сводится к сравнению соответствующих противопотоковых схем. Наиболее исследованными и часто применяемыми в неструктурированном случае являются противопотоковые схемы класса методов конечных объемов с расчетом переменных в центрах ячеек . Несмотря на то, что грани элементов разбиения не параллельны более координатным осям, данные схемы в большинстве случаев имеют одномерную природу, поскольку сводятся к решению задачи о распаде разрыва на линиях, соединяющих центроиды симплексов . Расчеты по подобным схемам не воспроизводят многомерную структуру потока и обладают чрезмерной численной диффузией . Для построения противопотоковых схем второго порядка аппроксимации необходимо существенное расширение шаблона, что в неструктурированном случае приводит к значительному усложнению соответствующих структур данных . Противопотоковые схемы для схем с расчетом неизвестных в узлах триангуляции и серединах ее ребер в настоящий момент немногочисленны (см. ). В ряде случаев противопотоковый принцип аппроксимации сводится к использованию одного значения скалярной субстанции - в узле симплекса, лежащем против потока , либо двух взвешенных значений - на концах ребра симплекса, лежащем против потока . Лишь одна из известных схем - схема, учитывающая направление потока (FLO, Flow Oriented Upwind Scheme), разработанная К. Пракашем и С. Патанкаром, - использует преимущество расчета неизвестных в узлах - возможность построения асимметричных функций профиля. Но расчеты по данной схеме признаны неудовлетворительными, поскольку схема не обладает свойством положительности, и итерационные процессы часто расходятся . Оценивание численной диффузии, привносимой использованием противопотоковых схем на симплициальных сетках, представляет собой самостоятельную проблему. Существующие работы в данном направлении, предоставляющие теоретические оценки характеристик сходимости, ограничены множеством схем расчетом переменных в центрах ячеек . Поэтому оценивание скорости сходимости противопотоковых схем МКО/КЭ с использованием серий численных экспериментов приобретает особое значение. Итак, построение и сравнительный анализ противопотоковых схем МКО/КЭ на неструктурированных сетках представляют собой актуальную тему исследований. Целью работы является разработка вычислительных технологий методов конечных объемов, использующих конечноэлементные пространства, для аппроксимации задач конвективно-диффузионного типа. Для достижения поставленной цели были сформулированы следующие задачи исследования: 1) усовершенствование технологий дискретизации систем законов сохранения методом конечных объемов/конечных элементов на симплициальных сетках, использующим барицентрические разбиения в качестве двойственных; 2) разработка технологий аппроксимации задач конвективно-диффузионного типа с существенными первыми производными; построение, реализация и сравнительный анализ противопотоковых схем на неструктурированных сетках, в частности, проведение вычислительных экспериментов для оценки порядка аппроксимации предлагаемых и наиболее точных известных схем, а также сравнение характеристик противопотоковых схем на базе МКО/КЭ и МКЭ; 3) создание на основе разработанных технологий комплексов программ, позволяющих адекватно моделировать вязкие несжимаемые течения жидкостей и газов в геометрически сложных областях, в стационарном и нестационарном случаях. Методы исследования. Методы вычислительной математики. Сравнительный анализ технологий точного интегрирования полиномов в методах конечных элементов, конечных объемов/элементов, распределенных невязок. Экспериментальное оценивание скорости сходимости противопотоковых схем для задач, имеющих аналитическое решение. Расчеты на множестве сгущающихся конечноэлементных разбиений, с последующим анализом сходимости к экспериментальным данным. Научная новизна работы состоит в следующем: 1. Предлагается новая технология учета кусочно-полиномиального представления решения, коэффициентов переноса и источниковых членов при дискретизации начально-краевых задач методами конечных объемов/элементов, конечных объемов/конечных элементов и подобъемов. Технология основана на использовании разложения по базису конечноэле-ментных пространств в терминах барицентрических симплициальных координат, с дальнейшим точным интегрированием их одночленов. Для схем МКО/КЭ, МКО/Э с расчетом переменных в узлах триангуляций предложены три класса формул точного интегрирования одночленов барицентрических координат: по отрезкам двойственной сетки в элементе, по барицентрическим подобластям и отрезкам граничных ребер. Для методов подобъемов, использующих несогласованные конечноэлементные пространства, предлагается использовать принцип точного интегрирования базисных функций и получены соответствующие интегральные формулы. 2. Предложен способ построения противопотоковых схем МКО/КЭ на симплициальных сетках, основанный на раздельной аппроксимации потоков массы и значений скалярной субстанции на отрезках двойственной сетки. Введены понятия локальной матрицы весовых коэффициентов противопо-токовой схемы, внутренних по отношению к элементам схем, локальной положительности схем. Предложена противопотоковая схема экспоненциального класса, построен ее аналог для МКО с расчетом неизвестных в барицентрах симплексов. 3. Получены экспериментальные оценки скорости сходимости противопото-ковой схемы со взвешиванием потоков масс и предлагаемой схемы экспоненциального класса. На решениях погранслойного типа проведен анализ устойчивости построенных схем и их сравнение с противопотоковыми схемами МКЭ. 4. С использованием предложенных технологий аппроксимаций задач конвективно-диффузионного типа создан комплекс программ для моделирования вязких несжимаемых течений в естественных переменных скорость-давление и проведен ряд вычислительных экспериментов, подтверждающих эффективность построенных схем. Структура и объем диссертации. Диссертация состоит из введения, четырех глав, заключения, списка литературы, приложения и содержит 173 страниц, включая 10 таблиц и 51 рисунок. Список литературы содержит 117 наименований.
Похожие диссертационные работы по специальности «Математическое моделирование, численные методы и комплексы программ», 05.13.18 шифр ВАК
Численный метод расчета течений сжимаемого вязкого газа в широком диапазоне чисел Маха 2004 год, кандидат физико-математических наук Чирков, Денис Владимирович
Метод численного исследования обтекания пространственных конфигураций путём решения уравнений Навье-Стокса на основе схем высокого порядка точности 2010 год, доктор физико-математических наук Волков, Андрей Викторович
Численное моделирование движения вязкой несжимаемой жидкости со свободными границами обобщенным методом естественных соседей 2008 год, кандидат физико-математических наук Рейн, Татьяна Сергеевна
Разработка технологии высокоточных вычислений на базе спектрального метода конечных элементов 2007 год, кандидат физико-математических наук Попонин, Владимир Сергеевич
Исследование течений вязкой жидкости в каналах сложной формы 2002 год, кандидат физико-математических наук Фирсов, Дмитрий Константинович
Заключение диссертации по теме «Математическое моделирование, численные методы и комплексы программ», Войтович, Татьяна Викторовна
Заключение
Настоящая работа посвящена разработке вычислительных технологий методов конечных объемов на симплициальных сетках, использующих конечноэле-ментные пространства и барицентрические разбиения в качестве двойственных, для аппроксимации задач конвективно-диффузионного типа! В работе получены следующие основною результаты, выносимые на защиту:
1. Предложена новая технология учета кусочно-полиномиального представления решения, коэффициентов переноса и источниковых членов при дискретизации начально-краевых задач методами конечных объемов/элементов, конечных объемов/конечных элементов и подобъемов. Технология основана на использовании разложения по базису конечноэлементных пространств в терминах барицентрических симплициальных координат, с дальнейшим точным интегрированием их одночленов. Для схем МКО/КЭ, МКО/Э с расчетом переменных в узлах триангуляций предложены три класса формул точного интегрирования одночленов барицентрических координат: по отрезкам двойственной сетки в элементе, по барицентрическим подобластям и отрезкам граничных ребер. Для методов подобъемов, использующих несогласованные ко-нечноэлементные пространства, предлагается использовать принцип точного интегрирования базисных функций и получены соответствующие интегральные формулы.
2. Предложен способ построения противопотоковых схем МКО/КЭ на симплициальных сетках, основанный на раздельной аппроксимации потоков массы и значений скалярной субстанции на отрезках двойственной сетки. Введены понятия локальной матрицы весовых коэффициентов противопотоковой схемы, внутренних по отношению к элементам схем, локальной положительности схем. Предложена противопотоковая схема экспоненциального класса, построен ее аналог для МКО с расчетом неизвестных в барицентрах симплексов.
3. Получены экспериментальные оценки скорости сходимости противопотоко-вой схемы со взвешиванием потоков масс и предлагаемой схемы экспоненциального класса. На решениях погранслойного типа проведен анализ устойчивости построенных схем и их сравнение с противопотоковыми схемами МКЭ. Показано, что достроенные схемы МКО/КЭ позволяют значительно более точно отследить особенности погранслойных решений, чем схемы метода Петрова-Галеркина с асимметричными базисными функциями (полиномы Лежандра), конечноэлементные схемы Райса и Шнипке, а также комбинированные конечноэлементные схемы повышенного порядка аппроксимации, разработанных Т. Шэу, С. Вангом и С. Цаем.
4. С использованием предложенных схем аппроксимации задач конвективно-диффузионного типа создан комплекс программ для моделирования вязких несжимаемых течений в естественных переменных скорость-давление, на совмещенных сетках, с использованием интерполяционных полиномов давления и скорости одного порядка; проведен ряд вычислительных экспериментов, подтверждающих эффективность построенных схем.
5. Для эталонного течения в канале за обратным уступом впервые показано взаимодействие входного эффекта и эффекта использования противопотоковых аппроксимаций.
Итак, предлагаемая в работе технология дискретизации начально-краевых задач методом конечных элементов/конечных объемов на симплициальных сетках является эффективным способом аппроксимации систем законов сохранения, разработанные противопотоковые схемы имеют хорошие характеристики сходимости, а использование методов дискретизации системы уравнений Навье-Сто-кса с одинаковым порядком интерполяции для компонент вектора скорости-давления позволяет получить результаты, хорошо согласующиеся с экспериментальными данными. Классы методов конечных объемов/конечных элементов на симплициальных сетках, технологической основой которых является точное интегрирование одночленов барицентрических координат, являются эффективными методами моделирования вязких несжимаемых течений в областях со сложной геометрией границ.
Список литературы диссертационного исследования кандидат физико-математических наук Войтович, Татьяна Викторовна, 2000 год
1. Белоцерковский О.М., Численное моделирование в механике сплошных сред. М.: Наука. Глав. ред. физ-мат. литературы, 1984.
2. А. С. Болдарев, В. А- Гасилов. О. Г. Ольховская, К решению гиперболических уравнений на неструктурированных сетках // Математическое моделирование. 1996. Т. 8, №3. С. 51-78.
3. П. А. Войнович, Д. М. Шаров, Моделирование разрывных течений газа на неструктурированных сетках // Математическое моделирование. 1993. Т. 5. № 7, С.86-114.
4. Я. J1. Гурьева, Вычислительная технология метода конечных объемов // Дис. на соискание ученой степени канд. ф.-м. наук. Новосибирск. 1997. - 115с.
5. Жуков М. Ф., Солоненко О. П., Высокотемпературные запыленные струи в процессах обработки порошковых материалов. Новосибирск. ИТ СО РАН. 1990.
6. В. П. Ильин, Балансные разностные схемы повышенной точности на неравномерных прямоугольных сетках. Новосибирск. 1994. - 31 с- (Препринт/ВЦ СО РАН № 1031).
7. Ильин В. П., Туракулов А. А., Об интегро-балансных аппроксимациях трехмерных краевых задач. Новосибирск, 1993. - 24 с. - (Препринт/ВЦ СО РАН:. № 986).
8. В. М. Ковеня, Н. Н. Яненко, Метод расщепления в задачах газовой динамики. Новосибирск, Наука. 1989.
9. А. Ладыженская, Математические вопросы динамики вязкой несжимаемой жидкости. М.: Tqc. изд-во ф.-м. лит.- 1961 .
10. Д. Оден, Конечны^ элементы в нелинейной механике сплошных сред. М.: Мир, 1976.
11. Патанкар С., Численные методы решения задач теплообмена и динамики жидкости. -М.:. Энергоатомиздат, 1984.
12. Н.Писсанецки С. Технология разреженных матриц. М.: Мир. 1988.
13. Препарата Ф. Шеймос М. Вычислительная геометрия; Введение. М." Мир, 1984.
14. А. А. Самарский, Введение в теорию разностных схем. М.: Наука, 1971.
15. Л Сегерлинд, Применение метода конечных элементов М.: Мир. 1979
16. Н. К. Суканек, Р. П. Родес, Формулировка условия на оси симметрии при численном расчете симметричных течений // Ракетная техника и космонавтика, 1978. Т. 16. № 10). С. 96-98.
17. Р. Темам, Уравнения Навье-Стокса, Теория и численный анализ // М.: Мир. 1981.
18. К. Флетчер, Численные методы на основании метода Галеркина II М.: Мир, 1991
19. Д. Ши, Численные методы в задачах теплообмена. М.; Мир, 1988.
20. Г. Шлихтинг, Теория пограничного слоя. М.: Изд-во иностр. лит. 1956.
21. Э. П. Шурина, Т. В. Войтович, Анализ алгоритмов методов конечных элементов и конечного объема на неструктурированных сетках при решении уравнений Навье-Стокса // Вычислительные технологии. 1997. Т. 2. № 4. С. 84104.
22. Э. П. Шурина, О. П. Солоненко, Т. В. Войтович, Новая технология метода конечных объемов на симплициальных сетках для задач конвективно-диффузионного типа. Новосибирск. 1999. -51 е.- (Препринт/ ИТПМ СО РАН; № 8-99).
23. И. Ю. Чумаков, Использование различных условий для давления на выходной границе при расчете сложных внутренних течений несжимаемой жидкости на совмещенных сетках // Вестн. мол. ученых. Сер. Прикладная математика и механика. 1997. Т 1. С. 55-62.
24. Н. Н. Яненко, Метод дробных шагов решения многомерных задач математической физики. Новосибирск: Наука, 1967.
25. A Finite Element Primer. National Agency for Finite Element Methods & Standarts //NEL. Glasgow, 1986.
26. К. Ajmani, W- F Ng. M-S. Lion, Preconditioned conjugate gradient methods for the Navier-Stokes Equations//J. Comput. Phys. 1994. Vol. 1 10. P. 68-81.
27. F. Angrand, A Dervieux, Some explicit triangular finite element schemes for the Euler equations//Int. J. forNumer. Methods in Fluids. 1984. Vol. 4. P. 749-764.
28. P. Arminjon, A. Dervieux, Construction of TVD-Hke Artificial Viscosities on Two-Dimensional Arbitrary FEM Grids // J. Comput. Phys., 1993. Vol. 106. P. 176-198.
29. B. Armaly, F. Durst, J. C. F. Pereira, B. Schoenung, Experimental and theoretical investigation of backward-facing step flow //J. Fluid Mech. 1983. Vol. 127. 473496.
30. F. Babuska, Error bounds for finite element methods//Numer. Math. 1971 Vol.16. P. 322-333.
31. Babuska, B. A. Szabo, I. N. Katz, The p-version of the finite element method // SIAM J. Numer. Anal. 1981. Vol. 18. P. 516-544.
32. P. Balland, E. Suli, Analysis of the cell-vertex finite volume method for hyperbolic problems with variable coefficients // SIAM J. Numer. Anal. 1997. Vol. 34. P. 1127-1151.
33. R. E. Bank, B. D. Welfert, A posteriori error estimates for the Stokes problem // SIAM J. Numer. Anal. 1991. Vol. 28. P. 591-623.
34. T. J. Barth, D. C. Jespersen, The design and application of upwind schemes on unstructured meshes // AIAA paper 89-0336.
35. E. Barton, A numerical study of flow over a confined backward-facing step // Int. J. ForNumer. Methods in Fluids. 1995. Vol. 21. P. 653-665.
36. E. Barton, The entrance effect of laminar flow over a backward-facing step geometry // Int. J. forNumer. Methods in Fluids. 1995. Vol. 25. P. 633-644.
37. S. Benharbit, A. Chalabi, J. P Vila, Numerical viscosity and convergence of finite volume methods for conservation laws with boundary conditions // SIAM J. Nu-mer. Anal. 1995. Vol. 32. P 775-796.
38. Z. Cai, On the finite volume element method //Numer. Math. 1991 Vol. 58 P. 713735.
39. Z. Cai, S. McCormick, On the accuracy of the finite volume element method for diffusion equations on composite grids // SIAM J. Numer. Anal. 1990. Vol. 27. P. 636-655.
40. Z. Cai, J. Mandel, S. McCormick, The finite volume element method for diffusion equations on general triangulations // SIAM J. Numer. Anal. 1991 Vol 28. P. 392402.
41. M. C. Ciccoli, Adaptive Domain Decomposition Algorithms and Finite Volume/Finite Element Approximation for Advection-Diffusion Equations // Journal of Scientific Computing. 1996. Vol 11. P 299-341.
42. P. Chatzipantelidis, A finite volume method based on the Crouzeix-Raviart element for elliptic PDE"s in two dimensions //Numer. Math. 1999, Vol. 82. P. 409-432.
43. К. H. Chen, R H. Pletcher, Primitive variable- strongly implicit calculation procedure for viscous flows at all speeds //AIAA J. 1991. Vol. 29. P1241-1249.
44. S. Chou, D. Kwak, P. S. Vassilevski, Mixed Covolume methods for elliptic problems on triangular grids // SIAM J. Numer. Anal. 1998. Vol. 35. P. 1850-1861.
45. Christie, D. F. Griffiths, A. R. Mitchell and О. C. Zienkiewicz, Finite element methods for second order differential equations with significant first derivatives // Int. J. Numer. Methods Eng. 1976. Vol. 10. 1389-1396.
46. J.-P. Croisille, Finite Volume Box Schemes // Proc. of Second Intern. Symp. on Finite Volumes for Complex Applications, 19-22 July., 1999, Duisburg, Germany. HERMES Science Publications, Paris, 1999.
47. В. Cockburn, F. Coquel. P. G. Lefloch, Convergence of the finite volume method for multidimensional conservation laws // SIAM J. Numer. Anal. 1995. Vol. 32. 687-705.
48. L. Davidson, A pressure correction method for unstructured meshes with arbitrary control volumes // Int. J. for Numer. Methods in Fluids. 1998. Vol. 22. P. 265-281.
49. C. Debiez, A. Dervieux, К. Мег, B. Nkonga, Computation of unsteady flows with mixed finite volump/finite element upwind methods // Int. J. for Numer. Methods in Fluids. 1998. Vol. 27. P. 193-206.
50. M. Delanaye, J. A. Essers, Quadratic-reconstruction Finite volume scheme for Compressible flows on unstructured adaptive grids // AIAA Journal. 1997. Vol. 35. P. 631-639.
51. Dervieux A., Steady Euler simulation using unstuctured meshes // VKI Lectures series. 1985. № 1884-04.
52. Eisenberg M. A., Malvern L. E., On finite element integration in natural coordinates // Int. J. Numer. Methods Eng. 1973. Vol. 7. 574-575.
53. A. Fezoui, Class of implicite upwind schemes for Euler simulations with unstructured meshes//J. Сотр. Phys. 1989. Vol. 84. P. 174-206.
54. C. Gallo, G. Manzini, A mixed finite element/finite volume approach for solving biodegradation transport in groundwater // Int. J. for Numer. Methods in Fluids.1998. Vol. 26. P. 533-556.
55. Т. Gallouet, J. P. Vila, Finite volume schemes for conservation laws of mixed type // SIAM J. Numer. Anal. 1991. Vol. 28. P. 1548-1573.
56. P. M. Gresho, S. T. Chan, R. L. Lee, G. D. Upson, A modified finite element method for solving the time-dependent. Incompressible Navier-Stokes equations. Part 2: Applications // Int. J. for Numer. Methods in Fluids, 1984. Vol. 4. P. 619640.
57. A. Grundmann, H. M. Moller, Invariant integration formulas for я-simplex by combinatonal methods // SIAM J. Numer. Anal 1978 Vol. 15, P. 282-290.
58. W. Hackbusch, On first and second order box schemes // Computing. 1989. Vol. 41. P. 277-296.
59. L. P. Hackman, G. D. Raithby, A. B. Strong. Numerical predictions of flows over backward-facing steps // Int. J. for Numer. Methods in Fluids. 1984. Vol. 4. P. 71 1-724.
60. L. Hallo, C. Ribault, M. Buffat, An implicit mixed finite volume-finite-element method for solving 3D turbulent compressible flows // Int. J. for Numer Methods in Fluids, 1997. Vol. 25. P. 1241-1261.
61. F. H. Harlow, J. E. Welch, Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface // Phys. Fluids. 1965. Vol. 8. P. 21822189.
62. F. Ilinca, D. Pelletier, A. Garon, An adaptive finite element method for a two-equation turbulence model in wall-bounded flows // Int. J. for Numer. Methods in Fluids. 1997. Vol. 124. P 101-120.
63. E. Issman, G. Degrez, H. Deconinck, Implicit Upwind Residual-Distribution Euler and Navier-Stokes Solver on Unstructured Meshes // AIAA Journal, 1996. Vol. 34. P. 2021-2028.
64. J. P. Jessee, W. A. Fiveland, A cell-vertex algorithm for the incompressible Navier-Stokes equations on non-ortogonal grids // Int. J. for Numer. Methods in Fluids. 1996. Vol. 23. P. 271-293.
65. Jianguo H., Shitong X., On the finite volume element method for general self-adjoint elliptic problems // SIAM .J Numer. Anal. 1998. Vol. 35. P. 1762-1774.
66. M. Lallemand, H. Steve, A. Dervieux, Unstructured Multigridding by volume agglomeration: current status // Computers Fluids, 1992 Vol. 21. P. 397-433.
67. Y. Liu, M. Vinokur, Exact integration of polynomials and symmetric quadrature formulas over arbitrary polyhedral grids // J. Comput. Phys. 1998. Vol. 140. P. 122-147.
68. D. Marcum, Turbulence models for unstructured finite element calculations // Int. J. ForNumer. Methods in Fluids. 1995, Vol. 20. P. 803-817.
69. C. Masson, H. I. Saabas, B. R. Baliga, Co-located equal-order control-volume finite element method for two-dimensional axisymmetric incompressible fluid flow // Int J. For Numer. Methods in Fluids. 1994. Vol. 18. P. 1-26.
70. С. Mattiussi, An Analysis of Finite Volume. Finite Element and Finite Difference Methods Using Some Concepts from Algebraic Topology // J. Comput. Phys. 1997. Vol. 133. P. 289-309.
71. D. Mavriplis, Multigrid solution of two-dimensional Euler equations on unstructured triangular meshes // AIAA Journal, 1988. Vol 26. P. 824-831.
72. P. R. McHugh, D. A. Knoll, Fully coupled finite volume solutions of the incompressible Navier-Stpkes and energy equations using an inexact Newton method // Int. J. For Numer. Methods in Fluids. 1994. Vol. 19. P. 439-455.
73. Y. Murthy, S. Mathur, Periodic flow and heat transfer using ustructured meshes // Int. J. for Numer. Methods in Fluids. 1997. Vol. 25. P. 659-677.
74. S. Muzaferija, D. Gosman, Finite-Volume CFD Procedure and Adaptive Error Control Strategy fof Grids of Arbitrary Topology // J. Comput. Phys., 1997, Vol. 138. P. 766-787
75. P. Nithiarasu, О. C. Zienkiewlcz, В. V. K. Satya Sai, K. Morgan, R. Codina, M. Vazquez, Shock capturing viscosities for the general fluid mechanics algorithm // Int. J. for Numer. Methods in Fluids. 1998. Vol. 28. P. 1325-1353.
76. K. Ohmori, T. Ushijima, A technique of upstream type applied to a linear nonconforming finite element approximation of convective diffusion equations // R.A.I.R.O. Anal. Numer.
77. D. Pan, J. C. Cheng, Upwind finite volume Navier-Stokes Computations on Uns-ructured Triangular Meshes // AIAA Journal, 1993. Vol. 31. P. 1618-1625.
78. S. V. Potapov, A mixed FE FV algorithm in non-linear solid dynamics // Proc. of Second Intern. Symp. on Finite Volumes for Complex Applications. 19-22 July, 1999. Duisburg, Germany. - HERMES Science Publications. Paris. 1999. P. 271278.
79. C. Prakash, S. V. Patankar, A control volume-based finite-element method for solving the Navier-Stokes equations using equal-order velocity-pressure interpolation //Numer. Heat Transfer. 1985. Vol. 8. P. 259-280.
80. S. Ramadhyani, S. V. Patankar, Solution of the Poisson equation: comparison of the Galerkin and control-volume methods // Int. J. Numer. Methods Eng. 1980. Vol. 15.1395-1418.
81. Rida S., McKenty F., Meng F. L., Reggio M., A staggered control volume scheme for unstructured triangular grids // Int. J. for Numer. Methods in Fluids. 1995. Vol. 25. P. 697-717.
82. P. L. Roe, Approximate Riemann Solvers, Parameter Vectors, and Difference Schemes//! Сотр. Phys. 1981. Vol. 43. P. 357-372.
83. C. Rohde, Upwind Finite volume schemes for weakly coupled hyperbolic systems of conservation laws in 2D // Numer. Math. 1998. Vol. 81. P. 85-123.
84. Tony W. H. Sheu, S. K. Wang, S. F. Tsai, Development of a high-resolution scheme for a multi-dimensional advection-diffusion equation // J. Сотр. Phys. 1998. Vol. 144. P. 1-16.
85. Saad Y., Iterative Methods for Sparse Linear Systems. PSW Publishing Co., Boston, MA, 1995.
86. В. V. K. S. Sai, О. C. Zienkiewicz, M. T. Manzari, P. R. M. Lyra, K. Morgan, General purpose versus special algorithms for high-speed flows with shocks // Int. J. Numer. Meth. Fluids. 1998. Vol. 27. P. 57-80.
87. J. L. Sohn, Evaluation of FIDAP on some classical laminar and turbulent benchmarks // Int. J. for Numer. Methods in Fluids. 1988. Vol. 8. P. 1469-1490.
88. В Stoufflet, Investigation of generalized flux vector splitting for compressible flows on triangular meshes // Int. J. for Numer. Methods in Fluids. 1995. Vol. 20. P. 1047-1059.
89. B. Stoufflet. J. Periaux, F. Fezoui, A. Dervieux, Numerical simulation of 3-D hypersonic Euler flows around space vehicles using adapted finite elements // AIAA Paper 87-0560.
90. C. Taylor, P. Hood, A numerical solution of the Navier-Stokes equations using the finite element technique // Computers and Fluids. 1973. Vol. 1. P. 73-100.
91. Thomadakis M, Leschziner M., A pressure-correction method for the solution of incompressible viscous flows on unstructured grids // Int .J. for Numer Methods in Fluids. -1996. Vol. 22 P 581-601.
92. A. K. Verma, V. Eswaran, Overlapping control volume approach for convection-diffusion problems // Int. J. for Numer. Methods in Fluids. 1996. Vol. 23. P. 865-882.
93. M. M. T. Wang, T. W. H. Sheu, On a compact mixed-order finite element for solving the three-dimensional incompressible Navier-Stokes equations // Int. J. for Numer. Methods in Fluids. 1997. Vol. 25. P. 513-522.
94. M. M. T. Wang, T. W. H. Sheu, Implementation of a free boundary condition to Navier-Stokes equations // Int. J. Numer. Methods Heat and Fluid Flow, 1997. Vol.7. P. 95-111.
95. D. Winterscheidt, K. S. Surana, p-Version least squares finite element formulation for two-dimensional, incompressible fluid flow // Int. J. Numer. Meth. Fluids, 1994. Vol. 18. P. 43-69.
96. A. M. Winslow, Numerical solution of the quasilinear Poisson equation in a nonuniform triangle mesh // J. Comput. Phys. 1967. Vol. 2. 149-172.
97. A. Younes, R. Mose. P. Ackerer. G. Chavent, A new formulation of the mixed finite element method for solving elliptic and parabolic PDE with triangular elements // J. Comput. Phys., 1999. Vol. 149. P. 148-167.
98. P.J. Zwart, G. D. Raithby, M. J. Raw, The integrated space-time finite volume method and its application to moving boundary problems // J. Comput. Phys. 1999. Vol. 154. P. 497-519.
99. О. C. Zienkiewicz, The Finite Element Method in Engineering Science // McGraw-Hill London. 1971.
100. O.C. Zienkiewicz, R. Codina, A general algorithm for compressible and incompressible flow. Part 1: The split, characteristic based scheme // Int. J. Numer. Meth. Fluids. 1995. Vol. 20. P. 869-885.
101. С. M. Rhie and W. L. Chow, A numerical study of the turbulent flow past an isolated aerofoil with trailing edge separation // AIAA Paper No. 82-0998. 1982.
102. R. I. Issa, Solution of the implicitly discretized fluid flow equations by operator-splitting//J. Comput. Phys. Vol. 62. P. 40-65.1985.
103. J. Kim, S. J. Kline, J. P. Johnston, Investigation of a Reattaching Turbulent Shear Layer: Flow Over a Backward-Facing Step // Journal of Fluids Eng., Vol. 102, P. 302-308.117. http//www.ict.nsc.ru/linpar
Обратите внимание, представленные выше научные тексты размещены для ознакомления и получены посредством распознавания оригинальных текстов диссертаций (OCR). В связи с чем, в них могут содержаться ошибки, связанные с несовершенством алгоритмов распознавания. В PDF файлах диссертаций и авторефератов, которые мы доставляем, подобных ошибок нет.
Некоторое время назад я искал описание операций, процессов, происходящих в библиотеке численного моделирования OpenFOAM. Нашел много абстрактных описаний работы метода конечных объёмов, классических разностных схем, различных физических уравнений. Мне же хотелось узнать более детально - откуда в таком-то выходном файле на такой-то итерации получились эти значения, какие выражения стоят за теми или иными параметрами в файлах настроек fvSchemes, fvSolution?
Для тех, кому это тоже интересно - эта статья. Те, кто хорошо знаком с OpenFOAM или с методами в нём реализованными - пишите о найденных ошибках и неточностях в личку.
На хабре уже была пара статей про OpenFOAM:
Поэтому не буду останавливаться на том, что это «открытая (GPL) платформа для численнного моделирования, предназначенная для моделирования, связанного с решением уравнений в частных производных методом конечных объёмов, и широко используемая для решения задач механики сплошных сред».
Сегодня я на простом примере опишу операции, которые происходят в ходе расчёта в OpenFOAM.
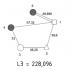
Итак, дана геометрия - куб со стороной 1 метр:
Перед нами стоит задача смоделировать поток-распространение некоторого скалярного поля (температура, количество вещества), который задаётся следующим уравнением переноса (1) внутри объема тела.
(1) ![]() ,
,
Где скалярная величина, например, выражает температуру [K] или концентрацию некоторого вещества, а выражает перенос вещества, массовый поток [кг/с].
Это уравнение, например, используют для моделирования распространения тепла![]() ,
,
где k - теплопроводность, а - температура [K].
Оператор дивергенции на самом деле это
оператор .
Напомню, что существует оператор набла (оператор Гамильтона), который записывается следующим образом:![]() ,
,
Где i, j, k - единичные векторы.
Если скалярно умножить оператор набла на векторную величину, то мы получим дивергенцию данного вектора:
«С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля»
Если умножить оператор набла на скаляр, получается градиент этого скаляра:
Градиент показывает увеличение или уменьшение по какому-либо направлению величины скаляра .
Граничные условия задачи следующие: есть грань-вход, грань-выход, остальные грани - гладкие стенки.

Разбиение объема куба на конечные объемы
Наша сетка будет очень простая - делим куб на 5 равных ячеек вдоль оси Z.
Много формул
Метод конечных объёмов предусматривает, что (1) в интегральной форме (2) будет выполняться для каждого конечного объёма .
(2)![]() ,
,
Где - геометрический центр конечного объёма.
Центр конечного объема

Упростим, преобразуем первое слагаемое выражения (2) следующим образом:
(2.1) (HJ-3.12)*
Как видно - мы приняли, что скалярная величина изменяется внутри конечного объема линейно и значение величины в некоторой точке внутри конечного объёма можно вычислить как:
Для упрощения второго слагаемого выражения (2) используем обобщённую теорему Гаусса-Остроградского : интеграл от дивергенции векторного поля по объёму , равен потоку вектора через поверхность , ограничивающую данный объём. На человеческом языке «сумма всех потоков в/из конечного объема равна сумме потоков через грани этого конечного объема»:
(2.3)![]() ,
,
Где замкнутая поверхность, ограничивающая объём ,
- вектор, направленный по нормали от объёма .
Вектор S

Учитывая то, что конечный объём ограничен набором плоских граней, можно выражение (2.3) преобразовать к сумме интегралов по поверхности:
(2.4) (HJ-3.13)
,
Где выражает значение переменной в центре грани,
- вектор площади, выходит из центра грани, направлен в сторону от ячейки (локально), в сторону от ячейки с меньшим индексом к ячейке с большим индексом (глобально).
Еще немного про вектор S
Чтобы не хранить одни и те же параметры вектора два раза, т.к. очевидно, что у двух соседних ячеек вектор-нормали к грани между ячейками, направленный в сторону От центра ячейки будет различаться только направлением-знаком. Поэтому было создано owner-neighbour отношение между гранью и ячейкой. Если вектор площади (глобальный, положительное направление от ячейки с меньшим индексом к ячейке с большим индексом) указывает ОТ центра ячейки такое отношение между ячейкой и вектором , а точнее между ячейкой и гранью, обозначается owner). В случае если этот вектор указывает внутрь рассматриваемой ячейки, то отношение neighbour. Направление влияет на знак величины (+ для owner и - для neighbour) и это важно при суммировании см. далее.
Про разностные схемы
Значение в центре грани вычисляется через значения в центрах прилегающих ячеек - способ такого выражения носит название разностной схемы. В OpenFOAM тип разностной схемы задается в файле /system/fvSchemes :DivSchemes { default none; div(phi,psi) Gauss linear; }
Gauss
- означает, что выбрана центральная разностная схема;
linear
- означает, что интерполяция с центров ячеек на центры граней будет происходить линейно.

Допустим, что наша скалярная величина изменяется внутри конечного объема от центра к граням линейно. Тогда аппроксимированное в центре грани значение будет вычисляться согласно формуле:
Где веса и рассчитываются как
Где - объемы ячеек.
Для случаев скошенных ячеек существуют более сложные формулы расчета весов аппроксимации.
Таким образом, значения phi_f в центрах граней ячеек вычисляются на основе значений в центрах ячеек. Значения градиентов grad(phi) вычисляются на основе значений phi_f.
И весь этот алгоритм может быть представлен в виде следующего псевдокода.
1. Объявляем массив градиентов конечных объемов, инициализируем его нулями
2. Пробегаемся по всем внутренним граням (которые не граничные)
> Вычисляем flux_f = phi_f*S_f. Значения phi_f вычисляем на основе значений phi в центах ячеек
> Добавляем flux_f к градиенту элемента-owner и -flux_f к градиенту элемента-neighbour
3. Пробегаемся по всем граничным граням
> Вычисляем flux_f = phi_f*S_f
> Добавляем flux_f к градиенту элементу-owner (neighbour-элементов у граничных граней нет)
4. Пробегаемся по всем элементам
> Делим получившуюся сумму-градиент на объем элемента
Дискретизация по времени

Учитывая (2.1) и (2.4) выражение (2) принимает вид:
(3)
Согласно методу конечных объёмов проводится дискретизация по времени и выражение (3) записывается как:
(4)
Проинтегрируем (4):
(4.1)![]()
Разделим левую и правую часть на :
(5)
Данные для матрицы дискретизации
Теперь мы можем получить систему линейных уравнений для каждого конечного объёма .Ниже представлена нумерация узлов сетки, которую мы будем использовать.
Координаты узлов хранятся в /constant/polyMesh/points
24
((0 0 0)
(1 0 0)
(0 1 0)
(1 1 0)
(0 0 0.2)
(1 0 0.2)
(0 1 0.2)
(1 1 0.2)
(0 0 0.4)
(1 0 0.4)
(0 1 0.4)
(1 1 0.4)
(0 0 0.6)
(1 0 0.6)
(0 1 0.6)
(1 1 0.6)
(0 0 0.8)
(1 0 0.8)
(0 1 0.8)
(1 1 0.8)
(0 0 1)
(1 0 1)
(0 1 1)
(1 1 1))
Нумерация узлов-центров ячеек (50, 51 - центры граничных граней):
Нумерация узлов-центров граней:
Объемы элементов:
Коэффициенты интерполяции, необходимые для вычисления значений на гранях ячеек. Индекс «e» обозначает «правая грань ячейки». Правая относительно вида, как на рисунке «Нумерация узлов-центров ячеек»:
Формирование матрицы дискретизации
Для P = 0.
Выражение (5), описывающее поведение величины

Будет преобразовано в систему линейных алгебраических уравнений, каждое из которых вида:
Или, согласно индексам точек на гранях
А еще все потоки в/из ячейки могут быть выражены в виде суммы

Где, например, - коэффициент линеаризации потока в точке-центре ячейки E,
- коэффициент линеаризации потока в точке-центре грани,
- нелинейная часть (например, константа).
Согласно нумерации граней выражение примет вид:
С учетом граничных условий для элемента P_0 линейное алгебраическое уравнение может быть представлено в виде
… подставим ранее полученные коэффициенты…

Поток из inlet"a направлен в ячейку, поэтому имеет отрицательный знак.
Так как у нас в управляющем выражении присутствует кроме диффузионного еще и временной член, но конечное уравнение выглядит как
Для P = 1.
Для P = 4.
Система линейных алгебраических уравнений (СЛАУ) может быть представлена в матричном виде как
A(i,j) === 40.5 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40 0.5 0 0 0 -0.5 40.5
Psi = dimensions ;
internalField nonuniform List
На основе которого получаются значения для вектора
Затем вектор подставляется в СЛАУ и происходит новая итерация расчёта вектора .
И так до тех пор, пока невязка не достигнет требуемых пределов.