Как определить центр тяжести тел неправильной формы. Нахождение центра тяжести своего тела. «Расчет конструкций на прочность»
Нарисуйте схему системы и отметьте на ней центр тяжести. Если найденный центр тяжести находится вне системы объектов, вы получили неверный ответ. Возможно, вы измерили расстояния от разных точек отсчета. Повторите измерения.
- Например, если на качелях сидят дети, центр тяжести будет где-то между детьми, а не справа или слева от качелей. Также центр тяжести никогда не совпадет с точкой, где сидит ребенок.
- Эти рассуждения верны в двумерном пространстве. Нарисуйте квадрат, в котором поместятся все объекты системы. Центр тяжести должен находиться внутри этого квадрата.
Проверьте математические вычисления, если вы получили маленький результат. Если точка отсчета находится на одном конце системы, маленький результат помещает центр тяжести возле конца системы. Возможно, это правильный ответ, но в подавляющем большинстве случаев такой результат указывает на ошибку. Когда вы вычисляли моменты, вы перемножали соответствующие веса и расстояния? Если вместо умножения вы сложили веса и расстояния, вы получите гораздо меньший результат.
Исправьте ошибку, если вы нашли несколько центров тяжести. Каждая система имеет только один центр тяжести. Если вы нашли несколько центров тяжести, скорее всего, вы не сложили все моменты. Центр тяжести равен отношению «суммарного» момента к «суммарному» весу. Не нужно делить «каждый» момент на «каждый» вес: так вы найдете положение каждого объекта.
Проверьте точку отсчета, если ответ отличается на некоторое целое значение. В нашем примере ответ равен 3,4 м. Допустим, вы получили ответ 0,4 м или 1,4 м, или другое число, оканчивающееся на «,4». Это потому, что в качестве точки отсчета вы выбрали не левый конец доски, а точку, которая расположена правее на целую величину. На самом деле, ваш ответ верен, независимо от того, какую точку отсчета вы выбрали! Просто запомните: точка отсчета всегда находится в положении x = 0. Вот пример:
- В нашем примере точка отсчета находилась на левом конце доски и мы нашли, что центр тяжести находится на расстоянии 3,4 м от этой точки отсчета.
- Если в качестве точки отсчета выбрать точку, которая расположена на расстоянии 1 м вправо от левого конца доски, вы получите ответ 2,4 м. То есть центр тяжести находится на расстоянии 2,4 м от новой точки отсчета, которая, в свою очередь, находится на расстоянии 1 м от левого конца доски. Таким образом, центр тяжести находится на расстоянии 2,4 + 1 = 3,4 м от левого конца доски. Получился старый ответ!
- Примечание: при измерении расстояния помните, что расстояния до «левой» точки отсчета отрицательные, а до «правой» – положительные.
Расстояния измеряйте по прямым линиям. Предположим, на качелях два ребенка, но один ребенок намного выше другого, или один ребенок висит под доской, а не сидит на ней. Проигнорируйте такую разницу и измерьте расстояния по прямой линии доски. Измерение расстояний под углами приведет к близким, но не совсем точным результатам.
- В случае задачи с качелями-доской помните, что центр тяжести находится между правым и левым концами доски. Позже вы научитесь вычислять центр тяжести более сложных двумерных систем.
Лекция 4. Центр тяжести.
В данной лекции рассматриваются следующие вопросы
1. Центр тяжести твердого тела.
2. Координаты центров тяжести неоднородных тел.
3. Координаты центров тяжести однородных тел.
4. Способы определения координат центров тяжести.
5. Центры тяжести некоторых однородных тел.
Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».
Приведение параллельных сил.
После того как было рассмотрено приведение к центру плоской системы и произвольной пространственной системы сил, мы опять возвращаемся к рассмотрению частного случая системы параллельных сил.
Приведение двух параллельных сил.
В ходе рассмотрения такой системы сил возможны три следующих случая приведения.
1. Система двух коллинеарных сил. Рассмотрим систему двух параллельных и направленных в одну сторону сил P и Q , приложенных в точках А и В . Будем считать, что силы перпендикулярны к этому отрезку (рис.1,а ).
С , принадлежащую отрезку АВ и удовлетворяющую условию:
АС /СВ = Q /P .(1)
Главный вектор системы R C = P + Q по модулюравен сумме этих сил:R C = P + Q .
С с учетом (1) равен нулю: M C = P ∙ АС - Q ∙ СВ = 0.
Таким образом, в результате приведения мы получили: R C ≠ 0, M C = 0. Это означает, что главный вектор эквивалентен равнодействующей, проходящей через центр приведения, то есть:
Равнодействующая коллинеарных сил равна по модулю их сумме, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внутренним образом.
Отметим, что положение точки С не изменится, если силы Р и Q повернуть на угол α . Точка С , обладающая таким свойством называется центром параллельных сил .
2. Система двух антиколлинеарных и не равных по модулю сил. Пусть силы P и Q , приложенные в точках А и В , параллельны, направлены в противоположные стороны и по модулю не равны (рис.1,б ).
Выберем в качестве центра приведения точку С , удовлетворяющую по-прежнему соотношению (1) и лежащую на той же прямой, но за пределами отрезка АВ .
Главный вектор этой системыR C = P + Q по модулю теперь будет равен разности модулей векторов:R C = Q - P .
Главный момент относительно центра С по-прежнему равен нулю: M C = P ∙ АС - Q ∙ СВ = 0, поэтому
Равнодействующая антиколлинеарных и не равных по модулю сил равна их разности, направлена в сторону большей силы, а ее линия действия делит отрезок, соединяющий точки их приложения, обратно пропорционально модулям этих сил внешнимобразом.
Рис.1
3. Система двух антиколлинеарных и равных по модулю сил. Возьмем за исходный предыдущий случай приведения. Зафиксируем силу Р , а силу Q устремим по модулю к силеР .
Тогда при Q → Р в формуле (1) отношение АС /СВ → 1. Это означает, чтоАС → СВ , то есть расстояние АС →∞ .
При этом модуль главного вектора R C → 0, а модуль главного момента не зависит от положения центра приведения и остается равным первоначальному значению:
M C = P ∙ АС - Q ∙ СВ = P ∙ ( АС - СВ ) = P ∙ А B .
Итак, в пределе мы получили систему сил, для которой R C = 0, M C ≠ 0, а центр приведения удален в бесконечность, которую нельзя заменить равнодействующей. В этой системе нетрудно узнать пару сил, поэтому пара сил равнодействующей не имеет .
Центр системыпараллельных сил.
Рассмотрим систему n сил P i , приложенных в точках A i (x i , y i , z i )и параллельных оси Ov c ортом l (рис.2).
Если заранее исключить случай системы, эквивалентной паре сил, нетрудно на основании предыдущего параграфа доказать существование ее равнодействующей R .
Определим координаты центра C (x c , y c , z c ) параллельных сил, то есть координаты точки приложения равнодействующейэтой системы.
Воспользуемся с этой целью теоремой Вариньона, на основании которой:
M 0 (R ) = Σ M 0 (P i ).

Рис.2
Вектор-момент силы можно представить в виде векторного произведения, поэтому:
М 0 (R ) = r c × R = Σ М 0i (P i ) = Σ (r i × P i ).
Учитывая, что R = R v ∙ l , а P i = P vi ∙ l и воспользовавшись свойствами векторного произведения, получим:
r c × R v ∙ l = Σ (r i × P vi ∙ l ),
r c ∙ R v × l = Σ (r i ∙ P vi × l ) = Σ (r i ∙ P vi ) × l ,
или:
[ r c R v - Σ (r i P vi )] × l = 0.
Последнее выражение справедливо только в том случае, если выражение в квадратных скобках равно нулю. Поэтому, опуская индекс v и учитывая, что равнодействующая R = Σ P i , отсюда получим:
r c = (Σ P i r i )/(Σ P i ).
Проектируя последнее векторное равенство на оси координат, получим искомое выражение координат центра параллельных сил :
x c = (Σ P i x i )/(Σ P i );
y c = (Σ P i y i )/(Σ P i );(2)
z c = (Σ P i z i )/(Σ P i ).
Центр тяжести тел.
Координаты центров тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆ V i , то на каждую его часть будет действовать сила притяжения ∆ P i , направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.3), и к ней применимы все выводы предыдущей главы.

Рис.3
Определение . Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
Напомним, что удельным весом элементарной части тела называется отношение ее веса ∆ P i к объему ∆ V i : γ i = ∆ P i / ∆ V i . Для однородного тела эта величина является постоянной: γ i = γ = P / V .
Подставляя в (2) ∆ P i = γ i ∙∆ V i вместо P i , учитывая последнее замечание и сокращая числитель и знаменатель на g , получим выражения координат центра тяжести однородного тела :
x c = (Σ ∆ V i ∙ x i )/(Σ ∆ V i );
y c = (Σ ∆ V i ∙ y i )/(Σ ∆ V i );(3)
z c = (Σ ∆ V i ∙ z i )/(Σ ∆ V i ).
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой плоскости.
Если оси х и у расположить в этой плоскости симметрии, то для каждой точки с координатами . И координата по (3), будет равна нулю, т.к. в сумме все члены имеющие противоположные знаки, попарно уничтожаются. Значит центр тяжести расположен в плоскости симметрии.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
Действительно, в этом случае, если ось z провести по оси симметрии, для каждой точки с координатами можно отыскать точку с координатами и координаты и , вычисленные по формулам (3), окажутся равными нулю.
Аналогично доказывается и третья теорема.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
И ещё несколько замечаний.
Первое. Если тело можно разделить на части, у которых известны вес и положение центра тяжести, то незачем рассматривать каждую точку, а в формулах (3) P i – определять как вес соответствующей части и – как координаты её центра тяжести.
Второе. Если тело однородное, то вес отдельной части его , где - удельный вес материала, из которого сделано тело, а V i - объём этой части тела. И формулы (3) примут более удобный вид. Например,
И аналогично, где - объём всего тела.
Третье замечание. Пусть тело имеет вид тонкой пластинки площадью F и толщиной t , лежащей в плоскости Oxy . Подставляя в (3) ∆ V i = t ∙ ∆ F i , получим координаты центра тяжести однородной пластинки :
x c = (Σ ∆ F i ∙ x i ) / (Σ ∆ F i );
y c = (Σ ∆ F i ∙ y i ) / (Σ ∆ F i ).
z c = (Σ ∆ F i ∙ z i ) / (Σ ∆ F i ).
где – координаты центра тяжести отдельных пластин; – общая площадь тела.
Четвёртое замечание. Для тела в виде тонкого криволинейного стержня длиной L с площадью поперечного сечения a элементарный объем ∆ V i = a ∙∆ L i , поэтому координаты центра тяжести тонкого криволинейного стержня будут равны:
x c = (Σ ∆ L i ∙ x i )/(Σ ∆ L i );
y c = (Σ ∆ L i ∙ y i )/(Σ ∆ L i );(4)
z c = (Σ ∆ L i ∙ z i )/(Σ ∆ L i ).
где – координаты центра тяжести i -го участка; .
Отметим, что согласно определению центр тяжести - это точка геометрическая; она может лежать и вне пределов данного тела (например, для кольца).
Примечание.
В этом разделе курса мы не делаем разницы между силой притяжения, силой тяжести и весом тела. В действительности сила тяжести представляет собой разность между силой притяжения Земли и центробежной силой, вызванной ее вращением.
Координаты центров тяжести неоднородных тел.
Координаты центра тяжести неоднородного твердого тела (рис.4) в выбранной системе отсчета определяются следующим образом:

Рис.4



где - вес единицы объема тела (удельный вес)
![]() -вес всего тела.
-вес всего тела.
неоднородную поверхность (рис.5), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.5



где - вес единицыплощади тела,
![]() -вес всего тела.
-вес всего тела.
Если твердое тело представляет собой неоднородную линию (рис.6), то координаты центра тяжести в выбранной системе отсчета определяются следующим образом:

Рис.6



где - вес единицыдлины тела,
Вес всего тела.
Способы определения координат центра тяжести.
Исходя из полученных выше общих формул,можно указать конкретные способы определения координат центров тяжести тел .
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.7), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

Рис.7
2. Разбиение. Тело разбивается на конечное число частей (рис.8), для каждой из которых положение центра тяжести и площадь известны.
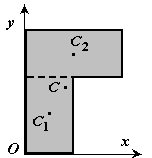
Рис.8
S =S 1 +S 2 .
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.9). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки(без выреза) с площадью S 1 и площади вырезанной части S 2 .

Рис.9
S = S 1 - S 2 .
4. Метод группировки. Является хорошим дополнением двух последних методов. После разбиения фигуры на составные элементы часть их бывает удобно объединить вновь, чтобы затем упростить решение путем учета симметрии этой группы.
Центры тяжести некоторых однородных тел.
1) Центр тяжести дуги окружности. Рассмотрим дугу АВ радиуса R с центральным углом . В силу симметрии центр тяжести этой дуги лежит на оси Ox (рис. 10).

Рис.10
Найдем координату по формуле . Для этого выделим на дуге АВ элемент ММ ’ длиною , положение которого определяется углом . Координата х элемента ММ’ будет . Подставляя эти значения х и dl и имея в виду, что интеграл должен быть распространен на всю длину дуги, получим:
![]()
где L - длина дуги АВ , равная .
Отсюда окончательно находим, что центр тяжести дуги окружности лежит на ее оси симметрии на расстоянии от центра О , равном
где угол измеряется в радианах.
2) Центр тяжести площади треугольника. Рассмотрим треугольник, лежащий в плоскости Oxy , координаты вершин которого известны: A i (x i ,y i ), (i = 1,2,3). Разбивая треугольник на узкие полоски, параллельные стороне А 1 А 2 , придем к выводу, что центр тяжести треугольника должен принадлежать медиане А 3 М 3 (рис.11) .

Рис.11
Разбивая треугольник на полоски, параллельные стороне А 2 А 3 , можно убедиться, что он должен лежать на медиане А 1 М 1 . Таким образом, центр тяжести треугольника лежит в точке пересечения его медиан , которая, как известно, отделяет от каждой медианы третью часть, считая от соответствующей стороны.
В частности, для медианы А 1 М 1 получим, учитывая, что координаты точки М 1 - это среднее арифметическое координат вершин А 2 иА 3 :
x c = x 1 + (2/3) ∙ (x М 1 - x 1 ) = x 1 + (2/3) ∙ [(x 2 + x 3 )/2 - x 1 ] = (x 1 + x 2 + x 3 )/3.
Таким образом, координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин:
x c =(1/3) Σ x i ; y c =(1/3) Σ y i .
3) Центр тяжести площади кругового сектора. Рассмотрим сектор круга радиуса R с центральным углом 2 α , расположенный симметрично относительно оси Ox (рис.12) .
Очевидно, что y c = 0, а расстояние от центра круга, из которого вырезан этот сектор, до его центра тяжести можно определить по формуле:

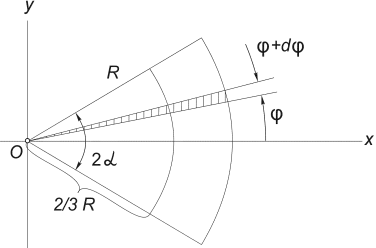
Рис.12
Проще всего этот интеграл вычислить, разбивая область интегрирования на элементарные секторы с углом d φ . С точностью до бесконечно малых первого порядка такой сектор можно заменить треугольником с основанием, равным R × d φ и высотой R . Площадь такого треугольника dF =(1/2)R 2 ∙ d φ , а его центр тяжести находится на расстоянии 2/3R от вершины, поэтому в (5) положим x = (2/3)R ∙ cosφ . Подставляя в (5) F = α R 2 , получим:
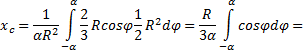
С помощью последней формулы вычислим, в частности, расстояние до центра тяжести полукруга .
Подставляя в (2) α = π /2, получим: x c = (4 R )/(3 π ) ≅ 0,4 R .
Пример 1. Определим центр тяжести однородного тела, изображённого на рис. 13.

Рис.13
Решение. Тело однородное, состоящее из двух частей, имеющих симметричную форму. Координаты центров тяжести их:
Объёмы их:
Поэтому координаты центра тяжести тела
Пример 2. Найдем центр тяжести пластины, согнутой под прямым углом. Размеры – на чертеже (рис.14).

Рис.14
Решение. Координаты центров тяжести:
0.
Площади:
Поэтому:
Пример 3.
У квадратного листа
см вырезано
квадратное отверстие
см (рис.15).
Найдем центр тяжести листа.
Пример 4.
Найти
положение центра тяжести пластинки, представленной на рис. 16. Размеры даны в
сантиметрах.

Рис.16
Решение. Разделим пластинку на фигуры (рис. 17), центры тяжести которых известны.
Площади этих фигур и координаты их центров тяжести:
1) прямоугольник со сторонами 30 и 40 см, S 1 =30 ∙ 40=1200 см 2 ; х 1 =15 см; у 1 =20 см.
2) прямоугольный треугольник с основанием 50 см и высотой 40 см; S 2 =0,5 ∙ 50 ∙ 40= 1000 см 2 ; х 2 =30+50/3=46,7 см;у 2 = 40/3 =13,3 см;
3) половина круга окружности радиуса r = 20 см; S 3 =0,5 ∙π∙ 20 2 =628 см 2 ; х 3 =4 R /3 π =8,5 см; у
Решение. Напомним, что в физике плотность тела ρ и его удельный вес g связаны соотношением: γ = ρ g , где g - ускорение свободного падения. Чтобы найти массу такого однородного тела, нужно плотность умножить на его объем.

Рис.19
Термин «линейная» или «погонная» плотность означает, что для определения массы стержня фермы нужно погонную плотность умножить на длину этого стержня.
Для решения задачи можно воспользоваться методом разбиения. Представив заданную ферму в виде суммы 6 отдельных стержней, получим:
где L i длина i -го стержня фермы, а x i , y i - координаты его центра тяжести.
Решение этой задачи можно упростить, если сгруппировать 5 последних стержней фермы. Нетрудно видеть, что они образуют фигуру, имеющую центр симметрии, расположенный посредине четвертого стержня, где и находится центр тяжести этой группы стержней.
Таким образом, заданную ферму можно представить комбинацией всего двух групп стержней.
Первая группа состоит из первого стержня,для нее L 1 = 4 м, x 1 = 0 м, y 1 = 2 м. Вторая группа стержней состоит из пяти стержней, для нее L 2 = 20 м, x 2 = 3 м, y 2 = 2 м.
Координаты центра тяжести фермы находим по формуле:
x c = (L 1 ∙ x 1 + L 2 ∙ x 2 )/(L 1 + L 2 ) = (4∙0 + 20∙3)/24 = 5/2 м;
y c = (L 1 ∙ y 1 + L 2 ∙ y 2 )/(L 1 + L 2 ) = (4∙2 + 20∙2)/24 = 2 м.
Отметим, что центр С лежит на прямой, соединяющей С 1 и С 2 и делит отрезок С 1 С 2 в отношении: С 1 С /СС 2 = (x c - x 1 )/(x 2 - x c ) = L 2 / L 1 = 2,5/0,5.
Вопросы для самопроверки
- Что называется центром параллельных сил?
- Как определяются координаты центра параллельных сил?
- Как определить центр параллельных сил, равнодействующая которых равна нулю?
- Каким свойством обладает центр параллельных сил?
- По каким формулам вычисляются координаты центра параллельных сил?
- Что называется центром тяжести тела?
- Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
- Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
- Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга?
- Что называют статическим моментом площади?
- Приведите пример тела, центр тяжести которого расположен вне тела.
- Как используются свойства симметрии при определении центров тяжести тел?
- В чем состоит сущность способа отрицательных весов?
- Где расположен центр тяжести дуги окружности?
- Каким графическим построением можно найти центр тяжести треугольника?
- Запишите формулу, определяющую центр тяжести кругового сектора.
- Используя формулы, определяющие центры тяжести треугольника и кругового сектора, выведите аналогичную формулу для кругового сегмента.
- По каким формулам вычисляются координаты центров тяжести однородных тел, плоских фигур и линий?
- Что называется статическим моментом площади плоской фигуры относительно оси, как он вычисляется и какую размерность имеет?
- Как определить положение центра тяжести площади, если известно положение центров тяжести отдельных ее частей?
- Какими вспомогательными теоремами пользуются при определении положения центра тяжести?
В инженерной практике случается, что возникает необходимость вычислить координаты центра тяжести сложной плоской фигуры, состоящей из простых элементов, для которых расположение центра тяжести известно. Такая задача является частью задачи определения...
Геометрических характеристик составных поперечных сечений балок и стержней. Часто с подобными вопросами приходится сталкиваться инженерам-конструкторам вырубных штампов при определении координат центра давления, разработчикам схем погрузки различного транспорта при размещении грузов, проектировщикам строительных металлических конструкций при подборе сечений элементов и, конечно, студентам при изучении дисциплин «Теоретическая механика» и «Сопротивление материалов».
Библиотека элементарных фигур.

Для симметричных плоских фигур центр тяжести совпадает с центром симметрии. К симметричной группе элементарных объектов относятся: круг, прямоугольник (в том числе квадрат), параллелограмм (в том числе ромб), правильный многоугольник.
Из десяти фигур, представленных на рисунке выше, только две являются базовыми. То есть, используя треугольники и сектора кругов, можно скомбинировать почти любую фигуру, имеющую практический интерес. Любые произвольные кривые можно, разбив на участки, заменить дугами окружностей.
Оставшиеся восемь фигур являются самыми распространенными, поэтому они и были включены в эту своеобразную библиотеку. В нашей классификации эти элементы не являются базовыми. Прямоугольник, параллелограмм и трапецию можно составить из двух треугольников. Шестиугольник – это сумма из четырех треугольников. Сегмент круга — это разность сектора круга и треугольника. Кольцевой сектор круга — разность двух секторов. Круг – это сектор круга с углом α=2*π=360˚. Полукруг – это, соответственно, сектор круга с углом α=π=180˚.
Расчет в Excel координат центра тяжести составной фигуры.
Передавать и воспринимать информацию, рассматривая пример, всегда легче, чем изучать вопрос на чисто теоретических выкладках. Рассмотрим решение задачи «Как найти центр тяжести?» на примере составной фигуры, изображенной на рисунке, расположенном ниже этого текста.

Составное сечение представляет собой прямоугольник (с размерами a 1 =80 мм, b 1 =40 мм), к которому слева сверху добавили равнобедренный треугольник (с размером основания a 2 =24 мм и высотой h 2 =42 мм) и из которого справа сверху вырезали полукруг (с центром в точке с координатами x 03 =50 мм и y 03 =40 мм, радиусом r 3 =26 мм).
В помощь для выполнения расчета привлечем программу MS Excel или программу OOo Calc . Любая из них легко справится с нашей задачей!
В ячейках с желтой заливкой выполним вспомогательные предварительные расчеты .
В ячейках со светло-желтой заливкой считаем результаты .
Синий шрифт – это исходные данные .
Черный шрифт – это промежуточные результаты расчетов .
Красный шрифт – это окончательные результаты расчетов .
Начинаем решение задачи – начинаем поиск координат центра тяжести сечения.
Исходные данные:
1. Названия элементарных фигур, образующих составное сечение впишем соответственно
в ячейку D3: Прямоугольник
в ячейку E3: Треугольник
в ячейку F3: Полукруг
2. Пользуясь представленной в этой статье «Библиотекой элементарных фигур», определим координаты центров тяжести элементов составного сечения xci и yci в мм относительно произвольно выбранных осей 0x и 0y и запишем
в ячейку D4: =80/2= 40,000
xc 1 = a 1 /2
в ячейку D5: =40/2=20,000
yc 1 = b 1 /2
в ячейку E4: =24/2=12,000
xc 2 = a 2 /2
в ячейку E5: =40+42/3=54,000
yc 2 = b 1 + h 2 /3
в ячейку F4: =50=50,000
xc 3 = x 03
в ячейку F5: =40-4*26/3/ПИ()=28,965
yc 3 = y 03 -4* r3 /3/ π
3. Рассчитаем площади элементов F 1 , F 2 , F 3 в мм2, воспользовавшись вновь формулами из раздела «Библиотека элементарных фигур»
в ячейке D6: =40*80=3200
F 1 = a 1 * b 1
в ячейке E6: =24*42/2=504
F2 = a2 *h2 /2
в ячейке F6: =-ПИ()/2*26^2=-1062
F3 = -π/2*r3 ^2
Площадь третьего элемента – полукруга – отрицательная потому, что это вырез – пустое место!

Расчет координат центра тяжести:
4. Определим общую площадь итоговой фигуры F 0 в мм2
в объединенной ячейке D8E8F8: =D6+E6+F6=2642
F 0 = F 1 + F 2 + F 3
5. Вычислим статические моменты составной фигурыSx и Sy в мм3 относительно выбранных осей 0x и 0y
в объединенной ячейке D9E9F9: =D5*D6+E5*E6+F5*F6=60459
Sx = yc1 * F1 + yc2 *F2 + yc3 *F3
в объединенной ячейке D10E10F10: =D4*D6+E4*E6+F4*F6=80955
Sy = xc1 * F1 + xc2 *F2 + xc3 *F3
6. И в завершение рассчитаем координаты центра тяжести составного сеченияXc и Yc в мм в выбранной системе координат 0x — 0y
в объединенной ячейке D11E11F11: =D10/D8=30,640
Xc = Sy / F 0
в объединенной ячейке D12E12F12: =D9/D8=22,883
Yc =Sx /F0
Задача решена, расчет в Excel выполнен — найдены координаты центра тяжести сечения, составленного при использовании трех простых элементов!
Заключение.
Пример в статье был выбран очень простым для того, чтобы легче было разобраться в методологии расчетов центра тяжести сложного сечения. Метод заключается в том, что любую сложную фигуру следует разбить на простые элементы с известными местами расположения центров тяжести и произвести итоговые вычисления для всего сечения.
Если сечение составлено из прокатных профилей – уголков и швеллеров, то их нет необходимости разбивать на прямоугольники и квадраты с вырезанными круговыми «π/2»- секторами. Координаты центров тяжести этих профилей приведены в таблицах ГОСТов, то есть и уголок и швеллер будут в ваших расчетах составных сечений базовыми элементарными элементами (о двутаврах, трубах, прутках и шестигранниках говорить нет смысла – это центрально симметричные сечения).
Расположение осей координат на положение центра тяжести фигуры, конечно, не влияет! Поэтому выбирайте систему координат, упрощающую вам расчеты. Если, например, я развернул бы в нашем примере систему координат на 45˚ по часовой стрелке, то вычисление координат центров тяжести прямоугольника, треугольника и полукруга превратилось бы в еще один отдельный и громоздкий этап расчетов, который «в уме» не выполнишь.
Представленный ниже расчетный файл Excel в данном случае программой не является. Скорее – это набросок калькулятора, алгоритм, шаблон по которому следует в каждом конкретном случае составлять свою последовательность формул для ячеек с яркой желтой заливкой .
Итак, как найти центр тяжести любого сечения вы теперь знаете! Полный расчет всех геометрических характеристик произвольных сложных составных сечений будет рассмотрен в одной из ближайших статей в рубрике « ». Следите за новостями на блоге.
Для получения информации о выходе новых статей и для скачивания рабочих файлов программ прошу вас подписаться на анонсы в окне, расположенном в конце статьи или в окне вверху страницы.
После ввода адреса своей электронной почты и нажатия на кнопку «Получать анонсы статей» НЕ ЗАБЫВАЙТЕ ПОДТВЕРЖДАТЬ ПОДПИСКУ кликом по ссылке в письме, которое тут же придет к вам на указанную почту (иногда - в папку « Спам» )!
Несколько слов о бокале, монете и двух вилках, которые изображены на «значке-иллюстрации» в самом начале статьи. Многим из вас, безусловно, знаком этот «трюк», вызывающий восхищенные взгляды детей и непосвященных взрослых. Тема этой статьи – центр тяжести. Именно он и точка опоры, играя с нашим сознанием и опытом, попросту дурачат наш разум!
Центр тяжести системы «вилки+монета» всегда располагается на фиксированном расстоянии по вертикали вниз от края монеты, который в свою очередь является точкой опоры. Это положение устойчивого равновесия! Если покачать вилки, то сразу становится очевидным, что система стремится занять свое прежнее устойчивое положение! Представьте маятник – точка закрепления (=точка опоры монеты на кромку бокала), стержень-ось маятника (=в нашем случае ось виртуальная, так как масса двух вилок разведена в разные стороны пространства) и груз внизу оси (=центр тяжести всей системы «вилки+монета»). Если начать отклонять маятник от вертикали в любую сторону (вперед, назад, налево, направо), то он неизбежно под действием силы тяжести будет возвращаться в исходное устойчивое состояние равновесия (это же самое происходит и с нашими вилками и монетой)!
Кто не понял, но хочет понять – разберитесь самостоятельно. Это ведь очень интересно «доходить» самому! Добавлю, что этот же принцип использования устойчивого равновесия реализован и в игрушке ванька–встань-ка. Только центр тяжести у этой игрушки расположен выше точки опоры, но ниже центра полусферы опорной поверхности.
Всегда рад вашим комментариям, уважаемые читатели!!!
Прошу, УВАЖАЯ труд автора, скачивать файл ПОСЛЕ ПОДПИСКИ на анонсы статей.
Учебник для 7 класса
§ 25.3. Как найти центр тяжести тела?
Напомним, что центром тяжести называют точку приложения силы тяжести. Рассмотрим, как найти на опыте положение центра тяжести плоского тела - скажем, вырезанной из картона фигуры произвольной формы (см. лабораторную работу № 12).
Подвесим картонную фигуру с помощью булавки или гвоздя так, чтобы она могла свободно вращаться вокруг горизонтальной оси, проходящей через точку О (рис. 25.4, а). Тогда эту фигуру можно рассматривать как рычаг с точкой опоры О.
Рис. 25.4. Как найти на опыте центр тяжести плоской фигуры
Когда фигура находится в равновесии, действующие на нее силы уравновешивают друг друга. Это сила тяжести F т, приложенная в центре тяжести фигуры Т, и сила упругости F упр, приложенная в точке О (эта сила приложена со стороны булавки или гвоздя).
Эти две силы уравновешивают друг друга только при условии, что точки приложения этих сил (точки Т и О) лежат на одной вертикали (см. рис. 25.4, а). В противном случае сила тяжести будет поворачивать фигуру вокруг точки О (рис. 25.4, б).
Итак, когда фигура находится в равновесии, центр тяжести лежит на одной вертикали с точкой подвеса О. Это и позволяет определить положение центра тяжести фигуры. Проведем с помощью отвеса вертикаль, проходящую через точку подвеса (синяя линия на рис. 25.4, в). На проведенной линии лежит центр тяжести тела. Повторим этот опыт при другом положении точки подвеса. В результате мы получим вторую линию, на которой лежит центр тяжести тела (зеленая линия на рис. 25.4, г). Следовательно, на пересечении этих линий находится искомый центр тяжести тела (красная точка Г на рис. 25.4, г).
Примечание. Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести стержня находится на середине высоты. При решении задач используются следующие методы:
1. метод симметрии: центр тяжести симметричных фигур находится на оси симметрии;
2. метод разделения: сложные сечения разделяем на несколько простых частей, положение центров тяжести которых легко определить;
3. метод отрицательных площадей: полости (отверстия) рассматриваются как часть сечения с отрицательной площадью.
Примеры решения задач
Пример1. Определить положение центра тяжести фигуры, представленной на рис. 8.4.
Решение
 Разбиваем фигуру на три части:
Разбиваем фигуру на три части:


Аналогично определяется у С = 4,5 см.
 Пример 2.
Найти положение центра тяжести симметричной стержневой фермы ADBE
(рис. 116), размеры которой таковы: АВ =
6м, DE =
3 м и EF =
1 м.
Пример 2.
Найти положение центра тяжести симметричной стержневой фермы ADBE
(рис. 116), размеры которой таковы: АВ =
6м, DE =
3 м и EF =
1 м.
Решение
Так как ферма симметричная, то ее центр тяжести лежит на оси симметрии DF. При выбранной (рис. 116) системе координатных осей абсцисса центра тяжести фермы
![]()
Неизвестной, следовательно, является лишь ордината у С центра тяжести фермы. Для ее определения разбиваем ферму на отдельные части (стержни). Длины их определяются из соответствующих треугольников.
Из ΔAEF имеем
Из ΔADF имеем

Центр тяжести каждого стержня лежит в его середине, координаты этих центров легко определяются из чертежа (рис. 116).
Найденные длины и ординаты центров тяжести отдельных частей фермы заносим в таблицу и по формуле
определяем ординату у с центра тяжести данной плоской фермы.
Следовательно, центр тяжести С всей фермы лежит на оси DF симметрии фермы на расстоянии 1,59 м от точки F.
 Пример 3.
Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).
Пример 3.
Определить координаты центра тяжести составного сечения. Сечение состоит из листа и прокатных профилей (рис. 8.5).
Примечание. Часто рамы сваривают из разных профилей, создавая необходимую конструкцию. Таким образом, уменьшается расход металла и образуется конструкция высокой прочности.
Для стандартных прокатных профилей собственные геометрические характеристики известны. Они приводятся в соответствующих стандартах.
Решение
1. Обозначим фигуры номерами и выпишем из таблиц необходимые данные:
1 - швеллер № 10 (ГОСТ 8240-89); высота h = 100 мм; ширина полки b = 46 мм; площадь сечения А 1 = 10,9 см 2 ;
2 - двутавр № 16 (ГОСТ 8239-89); высота 160 мм; ширина полки 81 мм; площадь сечения А 2 - 20,2 см 2 ;
3 - лист 5x100; толщина 5 мм; ширина 100мм; площадь сечения A 3 = 0,5 10 = 5 см 2 .
2. Координаты центров тяжести каждой фигуры можно определить по чертежу.
Составное сечение симметрично, поэтому центр тяжести находится на оси симметрии и координата х С = 0.
3. Определение центра тяжести составного сечения:

Пример 4. Определить координаты центра тяжести сечения, показанного на рис. 8, а. Сечение состоит из двух уголков 56x4 и швеллера № 18. Выполнить проверку правильности определения положения центра тяжести. Указать его положение на сечении.
Решение

1. : два уголка 56 х 4 и швеллер № 18. Обозначим их 1, 2, 3 (см. рис. 8, а).
2. Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их С 1 , С 2 , С 3 .
3. Выберем систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков.
4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому х с = 0. Координату у с определим по формуле
![]()
Пользуясь таблицами приложения, определим площади каждого профиля и координаты центров тяжести:
Координаты у 1 и у 2 равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения у с :
5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С. Покажем расстояние у С = 2,43 см от оси х до точки С.
Поскольку уголки симметрично расположены, имеют одинаковую площадь и координаты, то А 1 = А 2 , у 1 = у 2 . Поэтому формула для определения у С может быть упрощена:
![]()
6. Выполним проверку. Для этого ось х проведем по нижнему краю полки уголка (рис. 8, б). Ось у оставим, как в первом решении. Формулы для определения х С и у С не изменяются:
![]()
Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:
Находим координату центра тяжести:
По найденным координатам х с и у с наносим на рисунок точку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами у с, найденными при первом и втором решении, составляет: 6,51 - 2,43 = 4,08 см.
Это равно расстоянию между осями х при первом и втором решении: 5,6 - 1,52 = 4,08 см.
Ответ: у с = 2,43 см, если ось х проходит через центры тяжести уголков, или у с = 6,51 см, если ось х проходит по нижнему краю полки уголка.
Пример 5. Определить координаты центра тяжести сечения, изображенного на рис. 9, а. Сечение состоит из двутавра № 24 и швеллера №.24а. Показать положение центра тяжести на сечении.

Решение
1. Разобьем сечение на профили проката : двутавр и швеллер. Обозначим их цифрами 1 и 2.
3. Укажем центры тяжести каждого профиля С 1 и С 2 , используя таблицы приложений.
4. Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра.
5. Определим координаты центра тяжести сечения. Координата у с = 0, так как ось х совпадает с осью симметрии. Координату х с определим по формуле
![]()
По табл. 3 и 4 прил. I и схеме сечения определим
![]()
Подставим числовые значения в формулу и получим
5. Нанесем точку С (центр тяжести сечения) по найденным значениям х с и у с (см. рис. 9, а).
Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 9, б. В результате решения получим х с = 11,86 см. Разница между значениями х с при первом и втором решении равна 11,86 - 6,11 = 5,75 см, что равно расстоянию между осями у при тех же решениях b дв /2 = 5,75 см.
Ответ: х с = 6,11 см, если ось у проходит через центр тяжести двутавра; х с = 11,86 см, если ось у проходит через левые крайние точки двутавра.
Пример 6. Железнодорожный кран опирается на рельсы, расстояние между которыми АВ = 1,5м (рис. 1.102). Сила тяжести тележки крана G r = 30 кН, центр тяжести тележки находится в точке С, лежащей на линии KL пересечения плоскости симметрии тележки с плоскостью рисунка. Сила тяжести лебедки крана Q л = 10 кН приложена в точке D. Сила тяжести противовеса G„=20 кН приложена в точке Е. Сила тяжести стрелы G c = 5 кН приложена в точке Н. Вылет крана относительно линии KL равен 2 м. Определить коэффициент устойчивости крана в ненагруженном состоянии и какой груз F можно поднять этим краном при условии, что коэффициент устойчивости должен быть не менее двух.
Решение
1. В ненагруженном состоянии у крана возникает опасность опрокидывания при повороте вокруг рельса А. Следовательно, относительно точки А момент устойчивости

2. Опрокидывающий момент относительно точки А создается силой тяжести противовеса, т. е.
3. Отсюда коэффициент устойчивости крана в ненагруженном состоянии
4. При нагрузке стрелы крана грузом F возникает опасность опрокидывания крана с поворотом около рельса В. Следовательно, относительно точки В момент устойчивости

5. Опрокидывающий момент относительно рельса В
6. По условию задачи эксплуатация крана разрешается при коэффициенте устойчивости k B ≥ 2 , т. е.
Контрольные вопросы и задания
1. Почему силы притяжения к Земле, действующие на точки тела, можно принять за систему параллельных сил?
2. Запишите формулы для определения положения центра тяжести неоднородных и однородных тел, формулы для определения положения центра тяжести плоских сечений.
3. Повторите формулы для определения положения центра тяжести простых геометрических фигур: прямоугольника, треугольника, трапеции и половины круга.
4.  Что называют статическим моментом площади?
Что называют статическим моментом площади?
5. Вычислите статический момент данной фигуры относительно оси Ox. h = 30 см; b = 120 см; с = 10 см (рис. 8.6).
6. Определите координаты центра тяжести заштрихованной фигуры (рис. 8.7). Размеры даны в мм.
7. Определите координату у фигуры 1 составного сечения (рис. 8.8).
При решении воспользоваться справочными данными таблиц ГОСТ «Сталь горячекатанная» (см. Приложение 1).